题目内容
13．一个空间几何体的三视图如图所示，则该几何体的体积为16．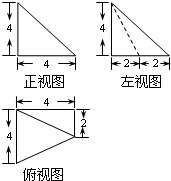
分析 由已知中的三视图，可知该几何体是一个以俯视图为底面的四棱锥，求出底面面积，代入棱锥体积公式，可得答案．
解答 解：由已知中的三视图，可知该几何体是一个以俯视图为底面的四棱锥，
其底面面积S=$\frac{1}{2}$（2+4）×4=12，
高h=4，
故棱锥的体积V=$\frac{1}{3}Sh$=16，
故答案为：16．
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
4．已知P为椭圆$\frac{{x}^{2}}{4}$+y2=1的左顶点，如果存在过点M（x0，0）（x0＞0）的直线交椭圆于A、B两点，使得S△AOB=2S△AOP，则x0的取值范围是（ ）
| A． | （1，$\sqrt{3}$] | B． | [$\sqrt{3}$，2） | C． | （1，2） | D． | （1，+∞） |
8．已知抛物线y2=4x的准线与双曲线$\frac{x^2}{3}-\frac{y^2}{b^2}=1$的一条准线重合，则这条抛物线y2=4x与双曲线$\frac{x^2}{3}-\frac{y^2}{b^2}=1$的交点P到抛物线焦点的距离为（ ）
| A． | $\sqrt{21}$ | B． | 21 | C． | 6 | D． | 4 |
18．要得到函数f（x）=sin（2x+$\frac{π}{4}$）的图象，只需将函数g（x）=sin2x的图象（ ）
| A． | 向左平移$\frac{π}{8}$个单位长度 | B． | 向右平移$\frac{π}{8}$个单位长度 | ||
| C． | 向左平移$\frac{π}{4}$个单位长度 | D． | 向右平移$\frac{π}{4}$个单位长度 |
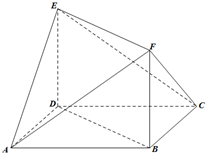如图，多面体ABCDEF中，DE⊥平面ABCD，底面ABCD是菱形，AB=2，
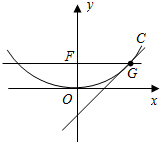设p＞0，抛物线方程为C：x2=2px．如图所示，过焦点F作x轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G的切线经过点（0，-1）．