题目内容
14.若偶函数f(x)=e${\;}^{-(x-m)^{2}}$(e是自然对数的底数)的最大值为n,则f(nm+mn)=$\frac{1}{e}$.分析 令t=-(x-m)2,则原函数化为g(t)=et,由复合函数的单调性可得原函数的增区间为(-∞,m),减区间为(m,+∞),即x=m时函数取得最大值n,由此求得n=1,f(x)=e${\;}^{-(x-m)^{2}}$是偶函数,可得m=0,即可得出结论.
解答 解:令t=-(x-m)2,则原函数化为g(t)=et,
内函数t=-(x-m)2在(-∞,m)上为增函数,在(m,+∞)上为减函数,
又外函数g(t)=et为增函数,
∴原函数的增区间为(-∞,m),减区间为(m,+∞),
∴当x=m时函数有最大值n=e0=1.
∵f(x)=e${\;}^{-(x-m)^{2}}$是偶函数,
∴m=0,
∴f(nm+mn)=f(1)=$\frac{1}{e}$.
故答案为:$\frac{1}{e}$.
点评 本题考查复合函数的单调性,复合的两个函数同增则增,同减则减,一增一减则减,注意对数函数的定义域是求解的前提,考查学生发现问题解决问题的能力,是中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.设函数f(x)=x2+ax+b.若方程f[f(x)]=0有四个不同的实数根x1,x2,x3,x4.且f(x1)=f(x2),x1+x2=-1.则实数b的取值范围是b<$-\frac{1}{4}$.
19.从装有若干个大小相同的红球、白球、黄球的袋中随机摸出1个球,摸到红球、白球、黄球的概率分别为$\frac{1}{2}$、$\frac{1}{3}$、$\frac{1}{6}$.从袋中随机摸出1个球,记下颜色后放回,连续摸3次,则记下的颜色中有红有黄但没有白的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{8}$ |
3.方程x2+y2+x+y-m=0表示一个圆,则m的取值范围是( )
| A. | (-$\frac{1}{2}$,+∞) | B. | (-∞,-$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$] | D. | [-$\frac{1}{2}$,+∞) |
4.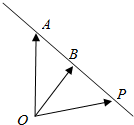 如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )
如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )
 如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )
如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )| A. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}+λ\overrightarrow{OB}}{1+λ}$(λ≠-1) | B. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}+λ\overrightarrow{OB}}{1-λ}$ | ||
| C. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}-λ\overrightarrow{OB}}{1+λ}$(λ≠-1) | D. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}-2λ\overrightarrow{OB}}{1-λ}$ |