题目内容
9.设函数f(x)=x2+ax+b.若方程f[f(x)]=0有四个不同的实数根x1,x2,x3,x4.且f(x1)=f(x2),x1+x2=-1.则实数b的取值范围是b<$-\frac{1}{4}$.分析 根据f(x1)=f(x2),x1+x2=-1.可得函数f(x)=x2+ax+b的图象关于直线x=-$\frac{1}{2}$对称,可得a=1,进而可得f(x3)=f(x4),x3+x4=-1.令f(x1)=f(x2)=m,f(x3)=f(x4)=n,则m+n=-1,m>f(-$\frac{1}{2}$),n>f(-$\frac{1}{2}$),解得答案.
解答 解:∵f(x1)=f(x2),x1+x2=-1.
故函数f(x)=x2+ax+b的图象关于直线x=-$\frac{1}{2}$对称,
即$-\frac{a}{2}$=-$\frac{1}{2}$,
故a=1,
则f(x3)=f(x4),x3+x4=-1.
令f(x1)=f(x2)=m,f(x3)=f(x4)=n,
则m+n=-1,m>f(-$\frac{1}{2}$),n>f(-$\frac{1}{2}$),
故-1>2f(-$\frac{1}{2}$)=$\frac{4b-1}{2}$,
解得:b<$-\frac{1}{4}$,
故答案为:b<$-\frac{1}{4}$
点评 本题考查的知识点是函数的零点与方程的根,二次函数的图象和性质,本题转化困难,属于难题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
20.设D为△ABC所在平面内一点,$\overrightarrow{AD}=2\overrightarrow{CD}$,则( )
| A. | $\overrightarrow{BD}=-\overrightarrow{BA}+2\overrightarrow{BC}$ | B. | $\overrightarrow{BD}=2\overrightarrow{BA}-\overrightarrow{BC}$ | C. | $\overrightarrow{BD}=\overrightarrow{BA}+2\overrightarrow{BC}$ | D. | $\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BA}+\frac{2}{3}\overrightarrow{BC}$ |
4.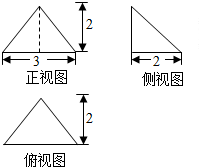 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )
 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )| A. | 6 | B. | 18 | C. | 8+3$\sqrt{2}$ | D. | 3+4$\sqrt{13}$ |