题目内容
4．
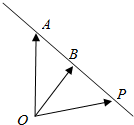如图，设一条直线上三点A，B，P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$（λ≠-1），O是平面上任意一点，则（ ）| A． | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}+λ\overrightarrow{OB}}{1+λ}$（λ≠-1） | B． | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}+λ\overrightarrow{OB}}{1-λ}$ | ||
| C． | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}-λ\overrightarrow{OB}}{1+λ}$（λ≠-1） | D． | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}-2λ\overrightarrow{OB}}{1-λ}$ |
分析 一条直线上三点A，B，P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$（λ≠-1），可得$\overrightarrow{OP}-\overrightarrow{OA}$=λ$（\overrightarrow{OB}-\overrightarrow{OP}）$，化简整理即可得出．
解答 解：∵一条直线上三点A，B，P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$（λ≠-1），
∴$\overrightarrow{OP}-\overrightarrow{OA}$=λ$（\overrightarrow{OB}-\overrightarrow{OP}）$，
化为$\overrightarrow{OP}$=$\frac{\overrightarrow{OA}+λ\overrightarrow{OB}}{1+λ}$．（λ≠1）．
故选：A．
点评 本题考查了向量共线定理、向量的三角形法则，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目