题目内容
2.已知sin($\frac{π}{3}-α$)=$\frac{1}{2}$,求cos($α+\frac{π}{3}$)•sin($\frac{2π}{3}+α$)的值.分析 由题意和平方关系求出cos($\frac{π}{3}-α$)的值,由两角差的余弦函数表示出cos(α+$\frac{π}{3}$),分别求出由诱导公式化简cos($α+\frac{π}{3}$)•sin($\frac{2π}{3}+α$),并求出cos($α+\frac{π}{3}$)•sin($\frac{2π}{3}+α$)的值.
解答 解:由sin($\frac{π}{3}-α$)=$\frac{1}{2}$得,cos($\frac{π}{3}-α$)=±$\sqrt{1-si{n}^{2}(\frac{π}{3}-α)}$=$±\frac{\sqrt{3}}{2}$,
∵$α+\frac{π}{3}$=$\frac{2π}{3}-(\frac{π}{3}-α)$,
∴cos(α+$\frac{π}{3}$)=cos[$\frac{2π}{3}-(\frac{π}{3}-α)$]
=cos$\frac{2π}{3}$cos($\frac{π}{3}-α$)+sin$\frac{2π}{3}$sin($\frac{π}{3}-α$)
当cos($\frac{π}{3}-α$)=$\frac{\sqrt{3}}{2}$时,cos($α+\frac{π}{3}$)=$-\frac{1}{2}×\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}×\frac{1}{2}$=0,
∴cos($α+\frac{π}{3}$)•sin($\frac{2π}{3}+α$)
=cos(α+$\frac{π}{3}$)•sin(π-$\frac{π}{3}$+α)
=cos(α+$\frac{π}{3}$)•sin($\frac{π}{3}$-α)=0;
当cos($\frac{π}{3}-α$)=-$\frac{\sqrt{3}}{2}$时,cos($α+\frac{π}{3}$)=$-\frac{1}{2}×(-\frac{\sqrt{3}}{2})+\frac{\sqrt{3}}{2}×\frac{1}{2}$=$\frac{\sqrt{3}}{2}$,
∴cos($α+\frac{π}{3}$)•sin($\frac{2π}{3}+α$)
=cos(α+$\frac{π}{3}$)•sin($\frac{π}{3}$-α)=$\frac{\sqrt{3}}{2}$×$\frac{1}{2}$=$\frac{\sqrt{3}}{4}$,
综上可得,cos($α+\frac{π}{3}$)•sin($\frac{2π}{3}+α$)的值是0或$\frac{\sqrt{3}}{4}$.
点评 本题考查平方关系、诱导公式,两角差的余弦函数,注意角之间的关系,考查化简、变形能力,属于中档题.


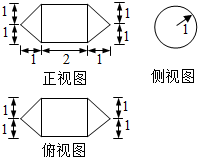 一个几何体的三视图如图所示则该几何体的体积为$\frac{8}{3}π$.
一个几何体的三视图如图所示则该几何体的体积为$\frac{8}{3}π$.