题目内容
12.某研究机构抽取五名高三学生甲、乙、丙、丁、戊,对他们的记忆力x和判断力y进行统计分析,得到的结果如表所示,根据表中的数据回答下列问题:| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| x | 6 | 8 | 10 | 12 | 14 |
| y | 2 | 3 | 4 | 5 | 6 |
(2)求记忆力x和判断力y的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并据此推测记忆力为20的学生的判断力大约是多少?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
分析 (1)确定基本事件的个数,利用古典概型概率公式,即可求解;
(2)利用公式求出a,b,可得回归直线方程,令x=20,即可得出结论.
解答 解:(1)从这五名学生中任选两名,共有${C}_{5}^{2}$=10种,选出的两名学生的记忆力均超过8有${C}_{3}^{2}$=3种,
∴从这五名学生中任选两名,选出的两名学生的记忆力均超过8的概率为$\frac{3}{10}$;
(2)由题意,$\overline{x}$=10,$\overline{y}$=4,∴b=$\frac{12+24+40+60+84-5×10×4}{36+64+100+144+196-5×100}$=0.5,
a=4-0.5×10=-1,∴y=0.5x-1,
x=20时,y=0.5×20-1=9,
点评 本题考查概率的计算,考查回归直线方程,考查学生的计算能力,正确计算是关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
3.在△ABC中,内角A,B,C的对边分别为a,b,c,已知A=2B,sinB=$\frac{\sqrt{7}}{4}$.若△ABC的面积S△ABC=$\frac{15\sqrt{7}}{4}$,则边AB的长为( )
| A. | 5 | B. | 6 | C. | 6$\sqrt{2}$ | D. | 8 |
1.设a>b>c>0,且a、b、c成等差数列,下列结论中错误的是( )
| A. | b+c,c+a,a+b成等差数列 | B. | $\frac{1}{a}$,$\frac{1}{b}$,$\frac{1}{c}$成等差数列 | ||
| C. | a2-bc,b2-ac,c2-ab成等差数列 | D. | $\frac{1}{\sqrt{a}+\sqrt{b}}$+$\frac{1}{\sqrt{b}+\sqrt{c}}$=$\frac{2}{\sqrt{a}+\sqrt{c}}$ |
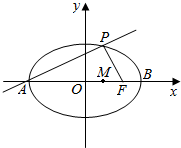 如图所示,点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF,设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|.
如图所示,点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF,设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|.