题目内容
7.设x>0,y>0且x+2y=1,f(x,y)=$\frac{1}{x}$+$\frac{1}{y}$+$\sqrt{\frac{1}{{x}^{2}}+\frac{1}{{y}^{2}}}$的最小值为10.分析 x>0,y>0,化简f(x,y)=$\frac{2}{x+y-\sqrt{{x}^{2}+{y}^{2}}}$,令m=$x+y-\sqrt{{x}^{2}+{y}^{2}}$,令x=ρcosθ,y=ρsinθ$(ρ>0,θ∈(0,\frac{π}{2}))$.利用x+2y=1,可得$ρ=\frac{1}{cosθ+2sinθ}$,可得(1-2m)sinθ+(1-m)cosθ=1,因此$\sqrt{(1-2m)^{2}+(1-m)^{2}}≥1$,化简解出即可.
解答 解:∵x>0,y>0,
∴f(x,y)=$\frac{1}{x}$+$\frac{1}{y}$+$\sqrt{\frac{1}{{x}^{2}}+\frac{1}{{y}^{2}}}$=$\frac{x+y}{xy}$+$\frac{\sqrt{{x}^{2}+{y}^{2}}}{xy}$=$\frac{x+y+\sqrt{{x}^{2}+{y}^{2}}}{xy}$=$\frac{2}{x+y-\sqrt{{x}^{2}+{y}^{2}}}$,
令m=$x+y-\sqrt{{x}^{2}+{y}^{2}}$,令x=ρcosθ,y=ρsinθ$(ρ>0,θ∈(0,\frac{π}{2}))$.
∵x+2y=1,∴$ρ=\frac{1}{cosθ+2sinθ}$,
∴m=ρ(cosθ+sinθ-1)=$\frac{cosθ+sinθ-1}{cosθ+2sinθ}$,
化为(1-2m)sinθ+(1-m)cosθ=1,
∴$\sqrt{(1-2m)^{2}+(1-m)^{2}}≥1$,化为5m2-6m+1≥0,
解得m≥1或m$≤\frac{1}{5}$,
∴f(x,y)≥10.
点评 本题考查了三角函数换元、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (-∞,0] | B. | [2,4] | C. | [4,+∞) | D. | {4} |
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| x | 6 | 8 | 10 | 12 | 14 |
| y | 2 | 3 | 4 | 5 | 6 |
(2)求记忆力x和判断力y的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并据此推测记忆力为20的学生的判断力大约是多少?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
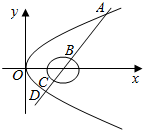 如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=14.
如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=14.