题目内容
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E为D1D的中点,AC与BD的交点为O.
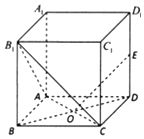
(1)求证:EO⊥平面AB1C;
(2)在由正方体的顶点确定的平面中,是否存在与平面AB1C平行的平面?证明你的结论
【答案】(1)见解析(2)存在平面A1C1D与平面AB1C平行.见解析
【解析】
(1)根据正方体的几何特征,易证 AC⊥平面BDD1B1,则AC⊥EO.在矩形BDD1B1中,利用勾股定理,有![]() ,即B1O⊥OE,再利用线面垂直的判定定理证明.
,即B1O⊥OE,再利用线面垂直的判定定理证明.
(2)存在平面A1C1D与平面AB1C平行.在正方体中,易得 A1C1∥平面AB1C,A1D∥平面AB1C,利用面面平行的判定定理证明.
(1)如图所示:连结B1D1,
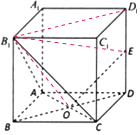
在正方体ABCD﹣A1B1C1D1中,AC⊥BD,BB1⊥AC,
又BB1平面BDD1B1,BD平面BDD1B1,且BB1∩BD=B,
所以AC⊥平面BDD1B1,
连结B1O,B1E,
又EO平面BDD1B1,则AC⊥EO.
在矩形BDD1B1中,设DD1=1,则![]() ,
,
所以![]() ,
,
则![]() ,即B1O⊥OE.
,即B1O⊥OE.
又B1O平面AB1C,EO平面AB1C,且B1O∩EO=O,
所以OE⊥平面AB1C;
(2)存在平面A1C1D与平面AB1C平行.
证明如下:在正方体ABCD﹣A1B1C1D1中,A1C1∥AC,A1D∥B1C,
又AC平面AB1C,B1C平面AB1C,A1C1平面AB1C,A1D平面AB1C,
所以A1C1∥平面AB1C,A1D∥平面AB1C,
又A1C1平面A1C1D,A1D平面A1C1D,且A1C1∩A1D=A1,
所以平面A1C1D∥平面AB1C.

【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:![]() ),经统计,其高度均在区间
),经统计,其高度均在区间![]() 内,将其按
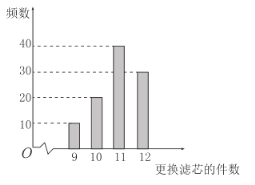
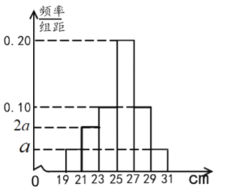
内,将其按![]() 分成6组,制成如图所示的频率分布直方图.其中高度为
分成6组,制成如图所示的频率分布直方图.其中高度为![]() 及以上的树苗为优质树苗.
及以上的树苗为优质树苗.
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
(1)求图中![]() 的值,并估计这批树苗高度的中位数和平均数(同一组数据用该组区间的中点值作代表);
的值,并估计这批树苗高度的中位数和平均数(同一组数据用该组区间的中点值作代表);
(2)已知所抽取的这120棵树苗来自于![]() ,
,![]() 两个试验区,部分数据如上列联表:将列联表补充完整,并判断是否有
两个试验区,部分数据如上列联表:将列联表补充完整,并判断是否有![]() 的把握认为优质树苗与
的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由.
两个试验区有关系,并说明理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
【题目】某次考试,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学物理分数对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
绘出散点图如下:

根据以上信息,判断下列结论:
①根据此散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据此散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③甲同学数学考了80分,那么,他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高.
其中正确的个数为( ).
A.0B.3C.2D.1