题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,线段
,线段![]() 的长为4.点
的长为4.点![]() 在椭圆
在椭圆![]() 上且位于第一象限,过点
上且位于第一象限,过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
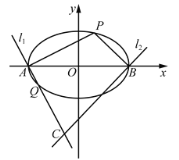
(1)若点![]() 的横坐标为-1,求点
的横坐标为-1,求点![]() 的坐标;
的坐标;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点为
的另一交点为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先求出椭圆的方程,设直线![]() 的方程为
的方程为![]() .分别表示出直线
.分别表示出直线![]() 与
与![]() 的方程,联立方程组,求出点
的方程,联立方程组,求出点![]() 的坐标,利用点
的坐标,利用点![]() 的横坐标为
的横坐标为![]() ,求出
,求出![]() ,进而可求出点
,进而可求出点![]() 的坐标;(2 )联立
的坐标;(2 )联立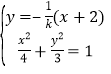 消去
消去![]() ,整理得
,整理得![]() ,求得
,求得![]() .由
.由![]() ,可得
,可得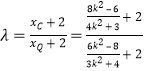
![]() ,结合
,结合![]() 即可求出
即可求出![]() 的取值范围.
的取值范围.
(1)设直线![]() 的斜率为
的斜率为![]() ,
,![]() ,
,
由题意得![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
因为点![]() 在椭圆
在椭圆![]() 上,且位于第一象限,
上,且位于第一象限,
所以![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
因为![]() ,
,
所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
联立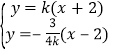 ,解得
,解得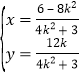 ,
,
即![]() .
.
因为![]() ,所以
,所以![]() ,
,
则直线![]() 的方程为
的方程为![]() .
.
因为![]() ,所以
,所以![]() .
.
则直线![]() 的方程为
的方程为![]() .
.
联立 ,解得
,解得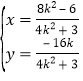 ,
,
即![]() .
.
因为点![]() 的横坐标为-1,
的横坐标为-1,
所以![]() ,解得
,解得![]() .
.
因为![]() ,
,
所以![]() .将
.将![]() 代入
代入![]() 可得,
可得,
点![]() 的坐标为
的坐标为![]() .
.
(2)设![]() ,
,![]() ,又直线
,又直线![]() 的方程为
的方程为![]() .
.
联立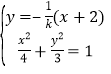 消去
消去![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,
解得![]() .
.
因为![]() ,
,
所以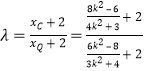
![]() .
.
因为![]() ,
,
所以![]() .
.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
【题目】2019年春节档有多部优秀电影上映,其中《流浪地球》是比较火的一部.某影评网站统计了100名观众对《流浪地球》的评分情况,得到如下表格:
评价等级 | ★ | ★★ | ★★★ | ★★★★ | ★★★★★ |
分数 | 0~20 | 2140 | 4160 | 61~80 | 81100 |
人数 | 5 | 2 | 12 | 6 | 75 |
(1)根据以上评分情况,试估计观众对《流浪地球》的评价在四星以上(包括四星)的频率;
(2)以表中各评价等级对应的频率作为各评价等级对应的概率,假设每个观众的评分结果相互独立.
(i)若从全国所有观众中随机选取3名,求恰有2名评价为五星1名评价为一星的概率;
(ii)若从全国所有观众中随机选取16名,记评价为五星的人数为X,求X的方差.