题目内容
【题目】在全球关注的抗击“新冠肺炎”中,某跨国科研中心的一个团队,研制了甲、乙两种治疗“新冠肺炎”新药,希望知道哪种新药更有效,为此进行动物试验,试验方案如下:
第一种:选取![]() 共10只患病白鼠,服用甲药后某项指标分别为:
共10只患病白鼠,服用甲药后某项指标分别为:![]() ;
;
第二种:选取![]() 共10只患病白鼠,服用乙药后某项指标分别为:
共10只患病白鼠,服用乙药后某项指标分别为:![]() ;
;
该团队判定患病白鼠服药后这项指标不低于85的确认为药物有效,否则确认为药物无效.
(1)已知第一种试验方案的10个数据的平均数为89,求这组数据的方差;
(2)现需要从已服用乙药的10只白鼠中随机抽取7只,记其中服药有效的只数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(3)该团队的另一实验室有1000只白鼠,其中900只为正常白鼠,100只为患病白鼠,每用新研制的甲药给所有患病白鼠服用一次,患病白鼠中有![]() 变为正常白鼠,但正常白鼠仍有
变为正常白鼠,但正常白鼠仍有![]() 变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用
变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用![]() 次甲药后此实验室正常白鼠的只数为
次甲药后此实验室正常白鼠的只数为![]() .
.
(i)求![]() 并写出
并写出![]() 与
与![]() 的关系式;
的关系式;
(ii)要使服用甲药两次后,该实验室正常白鼠至少有950只,求最大的正整数![]() 的值.
的值.
【答案】(1)6.2(2)见解析,![]() (3)
(3)![]() ,
,![]() (i)(ii)
(i)(ii)![]()
【解析】
(1)利用题设数据及方差的定义求解即可;
(2)利用超几何概型的概率公式计算概率,列分布列,即得解.
(3)(i)依题设知![]() ,即得解;
,即得解;
(ii)![]() ,代入
,代入![]() ,构造函数
,构造函数![]() 即得解.
即得解.
(1)方差![]()
(2)在第二种试验中服药有效的白鼠有4只,服药无效的白鼠有6只,
故![]() 的可能取值为1,2,3,4
的可能取值为1,2,3,4
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
因此![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 |
|
|
|
|
|
![]()
(3)(ⅰ)![]()
依题设知![]() ,
,
即![]()
(ⅱ)![]() ,
,
由![]() 可得
可得![]()
记函数![]() ,其中
,其中![]() ,
,
则函数![]() 在
在![]() 上单调递减,
上单调递减,
且![]() ,
,![]()
故最大的正整数![]()

 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | 18 | 30 |
非单车用户 | 38 | 32 | 70 |
合计 | 50 | 50 | 100 |
(1)从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
(2)将此样本的频率做为概率,从该市单车用户中随机抽取3人,记不小于40岁的单车用户的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: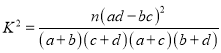 ,其中
,其中![]() )
)