��Ŀ����
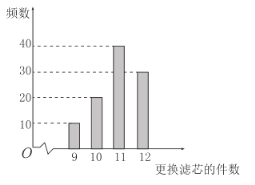
����Ŀ��ij�ͻ�������һ�������ľ�ˮ����ʹ������Ϊʮ�꣬�����ɺ��IJ�����о��ʵ��.��ʹ�ù����У���о��Ҫ�����ڸ�����������оÿ��200Ԫ.��ͼ�Ǹ���100̨�ÿˮ����ʮ��ʹ�����ڸ�������о�ļ����Ƴɵ���״ͼ.����100̨��ˮ��������о��Ƶ�ʴ���1̨��ˮ��������о�����ĸ��ʣ�
��1������һ̨��ˮ����ʹ�����ڸ�����о�ļ�������������λ��.
��2������һ̨��ˮ����ʹ�����ڸ�����о�ļ�������10�ĸ���.
��3����֪����100̨��ˮ���ڹ�����ͬʱ������о����5���Żݣ�ʹ�ù����������ٹ������Żݣ�������ÿ̨��ˮ���ڹ�����ͬʱ������о10������100̨��ˮ����ʹ�����ڣ�������о�ļ�����Ϊa��������ü�Ϊy����ȫ�±���������100̨��ˮ����ʹ�����ڹ�����о�����ܷ��õ�ƽ����.
100̨�ÿˮ�����������ڸ�����о�ļ���a | 9 | 10 | 11 | 12 |
Ƶ�� | ||||
����y |
���𰸡���1������Ϊ11����λ��Ϊ11����2��0.7����3����������1200Ԫ.
��������
��1��������ͼ����һ̨��ˮ����ʹ�����ڸ�����о�ļ�������������λ����
��2�������һ̨��ˮ����ʹ�����ڸ�����о�ļ�������10��Ƶ��Ϊ70��̨���������ùŵ���͵ĸ��ʹ�ʽ�ý⣻
��3����ͨ������õ���Ӧ�ķ���y,������ƽ�����Ĺ�ʽ���.
��1������һ̨��ˮ����ʹ�����ڸ�����о�ļ���������Ϊ11.
����һ̨��ˮ����ʹ�����ڸ�����о�ļ�������λ��Ϊ11.
��2����Ϊ��100̨��ˮ���У�һ̨��ˮ����ʹ�����ڸ�����о�ļ�������10��Ƶ��Ϊ![]() ��̨����
��̨����
���ԣ�һ̨��ˮ����ʹ�����ڸ�����о�ļ�������10��Ƶ��Ϊ![]() .
.
�ʹ���һ̨��ˮ����ʹ�����ڸ�����о�ļ�������10�ĸ���Ϊ0.7.
��3��![]() ʱ��
ʱ��![]() ��Ԫ��
��Ԫ��
![]() ʱ��
ʱ��![]() ��Ԫ��
��Ԫ��
![]() ʱ��
ʱ��![]() ��Ԫ��
��Ԫ��
![]() ʱ��
ʱ��![]() ��Ԫ��
��Ԫ��
��ȫ����ã�
100̨�ÿˮ����ʹ�����ڸ�����о�ļ���a | 9 | 10 | 11 | 12 |
Ƶ�� | 0.1 | 0.2 | 0.4 | 0.3 |
����y | 1000 | 1000 | 1200 | 1400 |
����ÿ̨��ˮ������һ����о10��������100̨��ˮ����ʹ�����ڹ�����о�����ܷ��õ�ƽ����Ϊ![]() ��Ԫ��
��Ԫ��

����Ŀ���ݡ����������������������Һ��պ���֣�NASA�����ijƣ����20��ǰ�����ø���ɫ�ˣ�����������ʾ�й���ӡ�ȵ��ж������˵������.��ͳ�ƣ��й������̻������![]() ������ֲ�����֣��±����й�ʮ��������ȥ��ֲ�����ֵ��������.�����������Ϊ�˹����֡��ɲ����֡��·�ɽ���֡��˻��������˹����µ����֮�ͣ�
������ֲ�����֣��±����й�ʮ��������ȥ��ֲ�����ֵ��������.�����������Ϊ�˹����֡��ɲ����֡��·�ɽ���֡��˻��������˹����µ����֮�ͣ�
�������
���� | ��������� | ���ַ�ʽ | ||||
�˹����� | �ɲ����� | �·�ɽ���� | �˻����� | �˹����� | ||
���� | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
�ӱ� | 583361 | 345625 | 33333 | 13507 | 65653 | 3643 |
���� | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
���� | 226333 | 100600 | 62400 | 63333 | ||
���� | 297642 | 184108 | 33602 | 63865 | 16067 | |
���� | 325580 | 260144 | 57438 | 7998 | ||
�½� | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
�ຣ | 178414 | 16051 | 159734 | 2629 | ||
���� | 91531 | 58960 | 22938 | 8298 | 1335 | |
���� | 19064 | 10012 | 4000 | 3999 | 1053 | |
��1��������������ݷֱ�д������ʮ���������˹��������������������ı�ֵ������С�ĵ�����
��2������ʮ�������У���ѡһ����������õ����·�ɽ�������ռ����������ı�ֵ����![]() �ĸ��ʣ�
�ĸ��ʣ�
��3������ʮ�������У����˻������������һ����ĵ����У���ѡ������������XΪ�������������˻������������������ĵ����ĸ�������X�ķֲ��м���ѧ����.