Question

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系中，曲线的参数方程为（为参数），曲线的参数方程为（为参数），在以为极点， 轴的正半轴为极轴的极坐标系中，射线，与， 各有一个交点，当时，这两个交点间的距离为2，当，这两个交点重合．

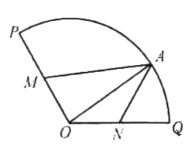
（1）分别说明， 是什么曲线，并求出与的值；

（2）设当时， 与， 的交点分别为，当， 与， 的交点分别为，求四边形的面积．

Answer 1

【答案】（1）详见解析；（2）

【解析】试题分析：（1）有曲线的参数方程为（为参数），曲线的参数方程为

（为参数），消去参数的是圆， 是椭圆，并利用．当时，这两个交点间的距离为，当时，这两个交点重合，求出及．（2）利用的普通方程，当时， 与的交点分别为，当时， 与的交点为，利用面积公式求出面积．

试题解析：（1）是圆， 是椭圆．

当时，射线与， 交点的直角坐标分别是因为这两点间的距离为2，所以

当，射线与， 交点的直角坐标分别是因为这两点重合，所以；

（2）， 的普通方程为

当时，射线与交点的横纵表是，与交点的横坐标是

当时，射线与， 的两个交点分别与交点关于轴对称，因此四边形为梯形，故四边形的面积为．