题目内容
【题目】已知函数f（x）=2sin （2x+ 
）．
（1）求函数f（x）的最小正周期及其单调减区间；
（2）用“五点法”画出函数g（x）=f（x），x∈[﹣ 
， 
]的图象（完成列表格并作图），由图象研究并写出g（x）的对称轴和对称中心．
【答案】
（1）解：函数f（x）=2sin （2x+ 
），
∴f（x）的最小正周期为T= 
=π；
令2kπ+ 
≤2x+ ≤2kπ+ 
，k∈Z，
则2kπ+ 
≤2x≤2kπ+ 
，k∈Z，
kπ+ ≤x≤kπ+ 
，k∈Z；
∴函数f（x）的单调减区间为[kπ+ ，kπ+ ]（k∈Z）；
（2）解：根据题意列出表格得：
x | ﹣ | ﹣ | ﹣ |
|
|
2x+ | ﹣π | ﹣ | 0 |
| π |
y=2sin（2x+ | 0 | ﹣2 | 0 | 2 | 0 |
根据表格画出函数g（x）=f（x），x∈[﹣ 
， 
]的图象如图所示，
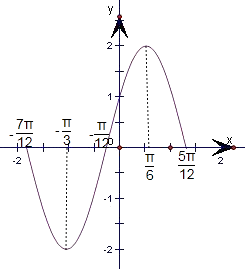
从图象上可以直观看出，此函数没有对称轴，有一个对称中心，对称中心是（﹣ 
，0）．
【解析】（1）根据正弦函数的图象与性质，求出f（x）的最小正周期与单调减区间；（2）根据题意列出表格，根据表格画出函数在x∈[﹣ ， ]的图象，结合图象得出此函数没有对称轴，有一个对称中心．
【考点精析】认真审题，首先需要了解五点法作函数y=Asin（ωx+φ）的图象(描点法及其特例—五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）)．
练习册系列答案
相关题目
