题目内容
【题目】如图，已知正三棱柱ABC=A1B1C1的各棱长都是4，E是BC的中点，动点F在侧棱CC1上，且不与点C重合．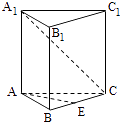
（1）当CF=1时，求证：EF⊥A1C；
（2）设二面角C﹣AF﹣E的大小为θ，求tanθ的最小值．
【答案】
（1）解：过E作EN⊥AC于N，连接EF，NF，AC1，由直棱柱的性质可知，底面ABC⊥侧面A1C
∴EN⊥侧面A1C
NF为EF在侧面A1C内的射影
则由 
，得NF∥AC1，又AC1⊥A1C，故NF⊥A1C
由三垂线定理可知EF⊥A1C
（2）解：连接AF，过N作NM⊥AF与M，连接ME
由（1）可知EN⊥侧面A1C，根据三垂线定理得EM⊥AF
∴∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=θ
设∠FAC=α则0°＜α≤45°，
在直角三角形CNE中，NE= 
，在直角三角形AMN中，MN=3sinα
故tanθ= 
，又0°＜α≤45°∴0＜sinα≤ 
故当α=45°时，tanθ达到最小值，
tanθ= 
，此时F与C1重合．
【解析】（1）过E作EN⊥AC于N，连接EF，NF，AC1 ， 根据面面垂直的性质可知NF为EF在侧面A1C内的射影，根据 ，得NF∥AC1 ， 又AC1⊥A1C，故NF⊥A1C，由三垂线定理可得结论；（2）连接AF，过N作NM⊥AF与M，连接ME根据三垂线定理得EM⊥AF，则∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=θ，在直角三角形CNE中，求出NE，在直角三角形AMN中，求出MN，故tanθ= ，根据α的范围可求出最小值．
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点，需要掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点才能正确解答此题．
