题目内容
【题目】某校有一块圆心![]() ,半径为200米,圆心角为
,半径为200米,圆心角为![]() 的扇形绿地
的扇形绿地![]() ,半径
,半径![]() 的中点分别为
的中点分别为![]() ,
,![]() 为弧
为弧![]() 上的一点,设
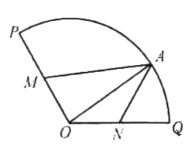
上的一点,设![]() ,如图所示,拟准备两套方案对该绿地再利用.
,如图所示,拟准备两套方案对该绿地再利用.
(1)方案一:将四边形绿地![]() 建成观赏鱼池,其面积记为
建成观赏鱼池,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式,并求
的函数关系式,并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
(2)方案二:将弧![]() 和线段
和线段![]() 围成区域建成活动场地,其面积记为
围成区域建成活动场地,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式;并求
的函数关系式;并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
【答案】(1)![]() ,当
,当![]() 时,
时,![]() (平方米);(2)
(平方米);(2)![]() ,
,![]() ,当
,当![]() 时,
时,![]() (平方米)
(平方米)
【解析】试题分析:首先表示四边形ANOM的面积,利用![]() 与
与![]() 面积相加,借助
面积相加,借助![]() 来表示,再根据三角函数求出最值,然后利用扇形
来表示,再根据三角函数求出最值,然后利用扇形![]() 的面积减去
的面积减去![]() 的面积表示ANQ的面积
的面积表示ANQ的面积![]() ,并借助导数求出最值.
,并借助导数求出最值.
试题解析:
(1)由已知,![]() ,
,![]() ,
,![]() ;
;
故![]() ,
,
整理得![]() (平方米),
(平方米),
∴当![]() 时,
时,![]() (平方米).
(平方米).
(2)由已知,![]() ,
,
∴![]() ,
,
即![]() ;
;
∴![]() ,故
,故![]() ;
;
∴![]() 在
在![]() 上为增函数,
上为增函数,
∴当![]() 时,
时,![]() (平方米).
(平方米).
答:(1)当![]() 时,
时,![]() (平方米);
(平方米);
(2)![]() 关于
关于![]() 的函数表达式
的函数表达式![]() ,
,![]()
当![]() 时,
时,![]() (平方米).
(平方米).

练习册系列答案
相关题目