题目内容
(本小题满分13分)
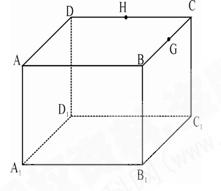
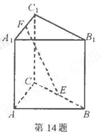
如图,在三棱柱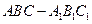 中,每个侧面均为正方形,
中,每个侧面均为正方形,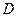 为底边
为底边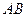 的中点,
的中点,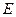 为侧棱
为侧棱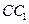 的中点,
的中点,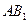 与
与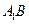 的交点为
的交点为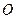 .
.
(Ⅰ)求证: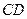 ∥平面
∥平面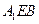 ;
;
(Ⅱ)求证: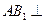 平面
平面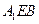 .
.
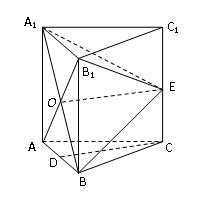
如图,在三棱柱
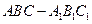 中,每个侧面均为正方形,
中,每个侧面均为正方形,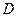 为底边
为底边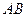 的中点,
的中点,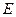 为侧棱
为侧棱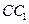 的中点,
的中点,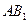 与
与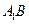 的交点为
的交点为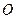 .
.(Ⅰ)求证:
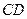 ∥平面
∥平面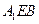 ;
; (Ⅱ)求证:
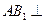 平面
平面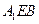 .
.
证明:(Ⅰ)设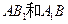 的交点为O,连接
的交点为O,连接 ,连接
,连接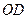 .
.
因为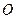 为
为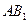 的中点,
的中点,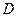 为
为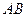 的中点,所以
的中点,所以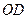 ∥
∥ 且
且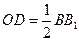 .
.
又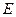 是
是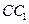 中点,
中点,
则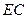 ∥
∥ 且
且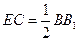 ,即
,即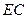 ∥
∥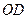 且
且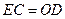 ,
,
则四边形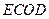 为平行四边形.所以
为平行四边形.所以 ∥
∥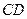 .
.
又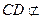 平面
平面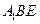 ,
,
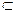 平面
平面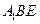 ,则
,则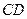 ∥平面
∥平面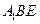 . ……………7分
. ……………7分
(Ⅱ) 因为三棱柱各侧面都是正方形,所以 ,
,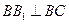 ,
,
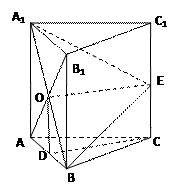 所以
所以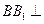 平面
平面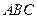 .
.
因为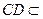 平面
平面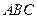 ,所以
,所以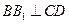 .
.
由已知得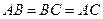 ,所以
,所以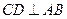 .
.
所以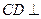 平面
平面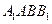 .
.
由(Ⅰ)可知 ∥
∥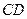 ,所以
,所以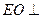 平面
平面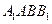 .
.
所以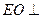
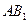 .
.
因为侧面是正方形,所以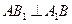 .
.
又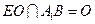 ,
,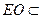 平面
平面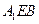 ,
,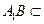 平面
平面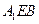 ,
,
所以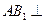 平面
平面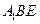 . ……………………………………………………13分
. ……………………………………………………13分
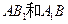 的交点为O,连接
的交点为O,连接 ,连接
,连接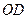 .
.因为
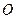 为
为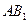 的中点,
的中点,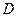 为
为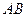 的中点,所以
的中点,所以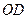 ∥
∥ 且
且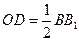 .
.又
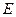 是
是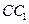 中点,
中点,则
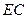 ∥
∥ 且
且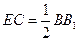 ,即
,即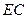 ∥
∥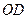 且
且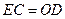 ,
,则四边形
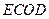 为平行四边形.所以
为平行四边形.所以 ∥
∥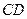 .
.又
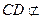 平面
平面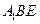 ,
,
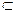 平面
平面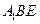 ,则
,则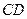 ∥平面
∥平面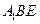 . ……………7分
. ……………7分(Ⅱ) 因为三棱柱各侧面都是正方形,所以
 ,
,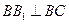 ,
, 所以
所以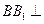 平面
平面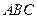 .
.因为
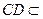 平面
平面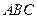 ,所以
,所以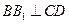 .
.由已知得
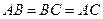 ,所以
,所以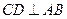 .
.所以
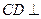 平面
平面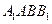 .
.由(Ⅰ)可知
 ∥
∥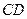 ,所以
,所以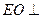 平面
平面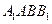 .
.所以
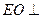
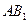 .
.因为侧面是正方形,所以
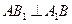 .
.又
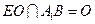 ,
,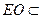 平面
平面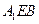 ,
,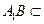 平面
平面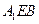 ,
,所以
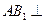 平面
平面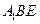 . ……………………………………………………13分
. ……………………………………………………13分略

练习册系列答案
相关题目
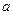 ,D为BC中点,M在BB1上,且
,D为BC中点,M在BB1上,且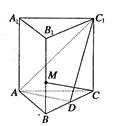
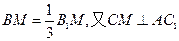 .
.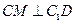 ;
;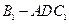 的体积.
的体积.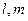 是两条不同的直线,
是两条不同的直线,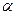 是一个平面,则下列命题错误的是 .
是一个平面,则下列命题错误的是 .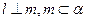 ,则
,则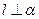 ;②若
;②若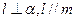 ,则
,则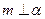 ;
;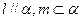 ,则
,则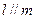 ;④若
;④若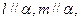 ,则
,则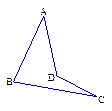
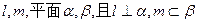 ,给出下列四个命题
,给出下列四个命题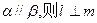 ;②若
;②若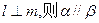 ;③若
;③若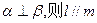 ;④若
;④若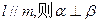
 和两条异面直线都平行的直线(
和两条异面直线都平行的直线(  )
)