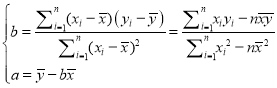题目内容
【题目】下列命题中,正确的为________(正确序号全部填上)
(1)空间中,一个角的两边与另一个角的两边分别平行,则这两个角相等或互补;
(2)一个二面角的两个半平面与另一个二面角的两个半平面分别垂直,则这两个二面角相等或互补;
(3)直线![]() ,
,![]() 为异面直线,所成角的大小为
为异面直线,所成角的大小为![]() ,过空间一点
,过空间一点![]() 作直线
作直线![]() ,使l与直线
,使l与直线![]() 及直线
及直线![]() 都成相等的角
都成相等的角![]() ,这样的直线可作3条;
,这样的直线可作3条;
(4)直线![]() 与平面
与平面![]() 相交,过直线
相交,过直线![]() 可作唯一的平面与平面
可作唯一的平面与平面![]() 垂直.
垂直.
【答案】(1)(3)
【解析】
(1)利用等角定理,即可判断正误;
(2)列举反例,即可得出结论;
(3)利用异面直线所成角,即可判断正误;
(4)列举反例,即可得出结论.
(1)空间中,若一个角的两边与另一个角的两边分别平行,
则由等角定理知,这两个角相等或互补,所以(1)正确;
(2)如图,平面![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,![]() ,且
,且![]() ,
,![]() ,
,
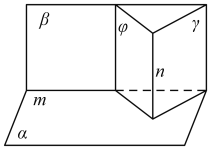
过直线![]() 作平面
作平面![]() ,此时
,此时![]() ,
,![]() ,
,
二面角![]() 为
为![]() ,而满足条件的平面
,而满足条件的平面![]() 有无穷多个,所以二面角
有无穷多个,所以二面角![]() 无法确定,
无法确定,
所以(2)错误;
(3)直线![]() ,
,![]() 为异面直线,所成角的大小为
为异面直线,所成角的大小为![]() ,过空间一点
,过空间一点![]() 作直线
作直线![]() ,
,
设直线l与直线![]() 及直线
及直线![]() 都成相等的角
都成相等的角![]() ,
,
若![]() ,可作0条;
,可作0条;
若![]() ,可作1条;
,可作1条;
若![]() ,可作2条;
,可作2条;
若![]() ,可作3条;
,可作3条;
若![]() ,可作4条;
,可作4条;
若![]() ,可作1条,
,可作1条,
所以(3)正确;
(4)若直线![]() 与平面
与平面![]() 垂直,过直线
垂直,过直线![]() 可作无数个平面与平面
可作无数个平面与平面![]() 垂直,所以(4)错误.
垂直,所以(4)错误.
故答案为:(1)(3).

【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为“喜爱打篮球与性别有关”?说明你的理由.
参考公式:独立性检测中,随机变量![]() ,
,
其中![]() 为样本容量
为样本容量
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: