题目内容
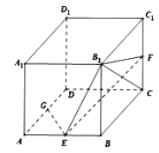
【题目】如图，在正三棱柱ABC-A1B1C1中，AB=3，AA1=4，M为AA1的中点，P是BC上的一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为
，设这条最短路线与CC1的交点为N．求：
（1）该三棱柱的侧面展开图的对角线的长；
（2）PC和NC的长．
【答案】(1)
(2) PC＝2, NC=
【解析】
（1）由题意结合展开图的特征求解其对角线长即可；
（2）首先画出其展开图，然后结合展开图的几何特征即可求得PC和NC的长．
（1）正三棱柱ABC-A1B1C1的侧面展开图是一个长为9，宽为4的矩形，
其对角线的长为
．
（2）
如图所示，将平面BB1C1C绕棱CC1旋转120°使其与侧面AA1C1C在同一平面上，点P运动到点P1的位置，连接MP1，则MP1就是由点P沿棱柱侧面经过棱CC1到点M的最短路线．
设PC=x，则P1C=x．
在Rt△MAP1中，
在勾股定理得(3+x)2+22=29，
求得x=2．
∴PC=P1C=2．
∵
=
，
∴NC=
【题目】为了解某地区某种农产品的年产量
（单位：吨）对价格
（单位：千元/吨）和利润
的影响，对近五年该农产品的年产量和价格统计如下表：
| 1 | 2 | 3 | 4 | 5 |
| 8 | 6 | 5 | 4 | 2 |
已知
和
具有线性相关关系.
（1）求
关于
的线性回归方程
；
（2）若每吨该农产品的成本为2.2千元，假设该农产品可全部卖出，预测当年产量为多少吨时，年利润
取到最大值？
参考公式： 
.
【题目】2018年，在《我是演说家》第四季这档节目中，英国华威大学留学生游斯彬的“数学之美”的演讲视频在微信朋友圈不断被转发，他的视角独特，语言幽默，给观众留下了深刻的印象．某机构为了了解观众对该演讲的喜爱程度，随机调查了观看了该演讲的140名观众，得到如下的列联表：（单位：名）
男 | 女 | 总计 | |
喜爱 | 40 | 60 | 100 |
不喜爱 | 20 | 20 | 40 |
总计 | 60 | 80 | 140 |
（1）根据以上列联表，问能否在犯错误的概率不超过0.05的前提下认为观众性别与喜爱该演讲有关．（精确到0．001）
（2）从这60名男观众中按对该演讲是否喜爱采取分层抽样，抽取一个容量为6的样本，然后随机选取两名作跟踪调查，求选到的两名观众都喜爱该演讲的概率．
附：临界值表
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式：
，
．
