题目内容
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: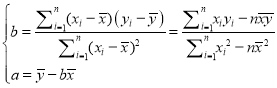
【答案】(1) y=0.7x+0.35;(2) 19.65吨.
【解析】
(1)利用回归直线方程计算公式,计算出回归直线方程.(2)令![]() ,求得改造后的能耗,用原来的能耗减去改造后的能耗,求得生产能耗比技改前降低的标准煤吨数.
,求得改造后的能耗,用原来的能耗减去改造后的能耗,求得生产能耗比技改前降低的标准煤吨数.
(1)由对照数据,计算得![]() ,
,![]() =4.5,
=4.5,![]() =3.5,
=3.5,
∴回归方程的系数为![]() =0.7,
=0.7,![]() =3.5-0.7×4.5=0.35,
=3.5-0.7×4.5=0.35,
∴所求线性回归方程为y=0.7x+0.35;
(2)由(1)求出的线性回归方程,
估计生产100吨甲产品的生产能耗为0.7×100+0.35=70.35(吨),
由90-70.35=19.65,
∴生产100吨甲产品的生产能耗比技改前降低19.65吨.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】2018年,在《我是演说家》第四季这档节目中,英国华威大学留学生游斯彬的“数学之美”的演讲视频在微信朋友圈不断被转发,他的视角独特,语言幽默,给观众留下了深刻的印象.某机构为了了解观众对该演讲的喜爱程度,随机调查了观看了该演讲的140名观众,得到如下的列联表:(单位:名)
男 | 女 | 总计 | |
喜爱 | 40 | 60 | 100 |
不喜爱 | 20 | 20 | 40 |
总计 | 60 | 80 | 140 |
(1)根据以上列联表,问能否在犯错误的概率不超过0.05的前提下认为观众性别与喜爱该演讲有关.(精确到0.001)
(2)从这60名男观众中按对该演讲是否喜爱采取分层抽样,抽取一个容量为6的样本,然后随机选取两名作跟踪调查,求选到的两名观众都喜爱该演讲的概率.
附:临界值表
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,
,![]() .
.