题目内容

【题目】选修4—4：坐标系与参数方程.

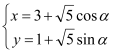已知曲线的参数方程为(为参数)，以直角坐标系原点为极点，轴正半轴为极轴建立极坐标系.

（1）求曲线的极坐标方程；

（2）若直线的极坐标方程为，求直线被曲线截得的弦长.

【答案】（1） （2）

【解析】

试题分析：（1） 利用，即可把参数方程转化为平面直角坐标系方程，然后在利用就可以把方程化成极坐标方程；

（2）由（1）知曲线的平面直角坐标系方程为圆的方程，直线的极坐标方程为为直线，然后利用弦长公式就可求解.

试题解析：（1）∵曲线的参数方程为 (为参数)

∴曲线的普通方程为

曲线 表示以 为圆心， 为半径的圆。

将 代入并化简：

即曲线的极坐标方程为 .

（2）∵的直角坐标方程为

∴圆心到直线的距离为

∴弦长为 .

练习册系列答案
相关题目

【题目】已知函数， .

（1）讨论函数的单调区间；

（2）求证： ；

（3）求证：当时， ， 恒成立.

【题目】如图1在△中，，、分别为线段、的中点，，．以为折痕，将△折起到图2的位置，使平面⊥平面，连接，，设是线段上的动点，满足．

（1）证明：平面⊥平面；

（2）若二面角的大小为，求的值．

【题目】已知函数， .

（1）讨论函数的单调区间；

（2）求证： ；

（3）求证：当时， ， 恒成立.

【题目】已知曲线

若，过点的直线交曲线于两点，且，求直线的方程；

若曲线表示圆，且直线与圆交于两点，是否存在实数，使得以为直径的圆过原点，若存在，求出实数的值；若不存在，请说明理由.

【题目】设圆上的点A(2,3)关于直线x＋2y＝0的对称点仍在圆上，且直线x－y＋1＝0被圆截得的弦长为2，求圆的方程．

【题目】已知直线的方程为，点是抛物线上到直线距离最小的点，点是抛物线上异于点的点，直线与直线交于点，过点与轴平行的直线与抛物线交于点.

（Ⅰ）求点的坐标；

（Ⅱ）证明直线恒过定点，并求这个定点的坐标.

【题目】为了解某地区某种农产品的年产量（单位：吨）对价格（单位：千元/吨）和利润的影响，对近五年该农产品的年产量和价格统计如下表：

（1）求关于的线性回归方程；

（2）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润取到最大值？（结果保留两位小数）

参考公式： ，

参考数据： ， .

【题目】如图，正方体中，分别为的中点.

（1）求证:平面⊥平面；

（2）当点在上运动时，是否都有平面，证明你的结论；

（3）若是的中点，求与所成的角的余弦值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网