��Ŀ����
13��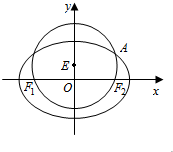 ��֪ԲE��x2+��y-$\frac{1}{2}$��2=$\frac{9}{4}$������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���F1��F2��������ԲC�ڵ�һ���Ľ���ΪA����F1��E��A���㹲�ߣ�ֱ��l����ԲC��M��N���㣬��$\overrightarrow{MN}$=��$\overrightarrow{OA}$���ˡ�0��
��֪ԲE��x2+��y-$\frac{1}{2}$��2=$\frac{9}{4}$������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���F1��F2��������ԲC�ڵ�һ���Ľ���ΪA����F1��E��A���㹲�ߣ�ֱ��l����ԲC��M��N���㣬��$\overrightarrow{MN}$=��$\overrightarrow{OA}$���ˡ�0����1������ԲC�ķ��̣�
��2����������AMN�����ȡ�����ֵʱ����ֱ��l�ķ��̣�
���� ��1��������ѽ����������Բ�ķ������c������������F1AΪԲE��ֱ�����|AF1|=3�����ݹ��ɶ������|AF2|��������Բ�Ķ����a2=b2+c2�������a��b��ֵ��������Բ���̼��ɣ�
��2���ɣ�1�����A�����꣬�����������ߵ��������ֱ��OA��б�ʣ���ֱ��l�ķ��̺�M��N�����꣬����ֱ�ߺ���Բ������ȥy������Τ�ﶨ�����ҳ���ʽ���|MN|���ɵ㵽ֱ�ߵľ��빫ʽ�����A��ֱ��l�ľ��룬���������ε������ʽ�����AMN�����S�ı���ʽ����������û�������ʽ�����������ֵ�Լ���Ӧ��m������ֱ��l�ķ��̼��ɣ�
��� 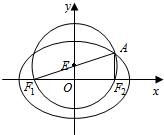 �⣺��1����ͼԲE������ԲC�����ҽ���F1��F2��
�⣺��1����ͼԲE������ԲC�����ҽ���F1��F2��
��c2+��0-$\frac{1}{2}$��2=$\frac{9}{4}$�����c=$\sqrt{2}$������2�֣�
��F1��E��A���㹲�ߣ���F1AΪԲE��ֱ������|AF1|=3��
��AF2��F1F2����$|A{F}_{2}{|}^{2}$=$|A{F}_{1}{|}^{2}$-$|{F}_{1}{F}_{2}{|}^{2}$=9-8=1��
��2a=|AF1|+|AF2|=3+1=4����a=2
��a2=b2+c2�ã�b=$\sqrt{2}$������4�֣�
����ԲC�ķ�����$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$������5�֣�
��2���ɣ�1���õ�A�����꣨$\sqrt{2}$��1����
��$\overrightarrow{MN}=��\overrightarrow{OA}$���ˡ�0������ֱ��l��б��ΪkOA=$\frac{\sqrt{2}}{2}$������6�֣�
����ֱ��l�ķ���Ϊy=$\frac{\sqrt{2}}{2}$x+m����M��x1��y1����N��x2��y2����
��$\left\{\begin{array}{l}{y=\frac{\sqrt{2}}{2}x+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$�ã�${x}^{2}+\sqrt{2}mx+{m}^{2}-2=0$��
��x1+x2=$-\sqrt{2}m$��x1x2=m2-2��
�ҡ�=2m2-4m2+8��0�����-2��m��2������8�֣�
��|MN|=$\sqrt{1+{k}^{2}}$|x2-x1|=$\sqrt{1+\frac{1}{2}}$$\sqrt{��{x}_{1}+{x}_{2}��^{2}-{4x}_{1}{x}_{2}}$
=$\sqrt{\frac{3}{2}}$$\sqrt{��-\sqrt{2}m��^{2}-4��{m}^{2}-2��}$=$\sqrt{{12-3m}^{2}}$��
�ߵ�A��ֱ��l�ľ���d=$\frac{|\frac{\sqrt{2}}{2}��\sqrt{2}-1+m|}{\sqrt{\frac{1}{2}+1}}$=$\frac{\sqrt{6}|m|}{3}$��
���AMN�����S=$\frac{1}{2}|MN|d$=$\frac{1}{2}��\sqrt{{12-3m}^{2}}��\frac{\sqrt{6}|m|}{3}$
=$\frac{\sqrt{2}}{2}$$\sqrt{{��4-m}^{2}��{m}^{2}}$��$\frac{\sqrt{2}}{2}��\frac{4-{m}^{2}+{m}^{2}}{2}$=$\sqrt{2}$������10�֣�
���ҽ���4-m2=m2����m=$��\sqrt{2}$��ֱ��l�ķ���Ϊ$y=\frac{\sqrt{2}}{2}x��\sqrt{2}$������12�֣�
���� ���⿼����Բ�ı����̣�Τ�ﶨ�����ҳ���ʽ�����������������Լ�ֱ�ߡ�Բ����Բ��λ�ù�ϵ�ȣ������֪ʶ�࣬�ۺ���ǿ�����黯����������������е��⣮

 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| A�� | 6 | B�� | 7 | C�� | 8 | D�� | 9 |
| A�� | ��99%������Ϊ����Ŀ���� | |
| B�� | ��99%������Ϊ����Ŀ�Ƿ�������ĸ��й�ϵ | |
| C�� | ��99%�İ�����Ϊ������Ŀ�Ƿ�������ĸ��й�ϵ | |
| D�� | û��������Ϊ������Ŀ�Ƿ�������ĸ��й�ϵ |
| A�� | {x|x��$\frac{1}{2}$} | B�� | {x|x��$\frac{1}{2}$��x��-$\frac{1}{2}$} | C�� | {x|x��$\frac{1}{2}$} | D�� | {x|x��$\frac{1}{2}$��x��-$\frac{1}{2}$} |
| A�� | ?x�ʣ�0��+�ޣ���2x��x2 | B�� | ?x�ʣ�0��+�ޣ���2x��x2 | C�� | ?x�ʣ�0��+�ޣ���2x��x2 | D�� | ?x�ʣ�0��+�ޣ���2x��x2 |