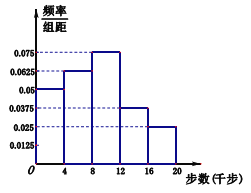
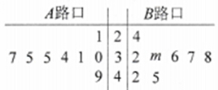
题目内容
【题目】正三棱锥P﹣ABC中,CM=2PM,CN=2NB,对于以下结论:
①二面角B﹣PA﹣C大小的取值范围是( ![]() ,π);
,π);
②若MN⊥AM,则PC与平面PAB所成角的大小为 ![]() ;
;
③过点M与异面直线PA和BC都成 ![]() 的直线有3条;
的直线有3条;
④若二面角B﹣PA﹣C大小为 ![]() ,则过点N与平面PAC和平面PAB都成
,则过点N与平面PAC和平面PAB都成 ![]() 的直线有3条.
的直线有3条.
正确的序号是 . 
【答案】①②④
【解析】解:①设底面正三角形的边长为1,过B作BD⊥PA,连结CD,则∠BDC是二面角B﹣PA﹣C大小,因为底面三角形ABC是正三角形,所以∠CAB= ![]() ,所以当点P无限靠近点O时,即高无限小时,∠BDC接近
,所以当点P无限靠近点O时,即高无限小时,∠BDC接近 ![]() ,所以二面角B﹣PA﹣C大小的取值范围是(
,所以二面角B﹣PA﹣C大小的取值范围是( ![]() ,π),所以①正确.
,π),所以①正确.
②因为CM=2PM,CN=2NB,所以MN∥PB.若MN⊥AM,则PB⊥AM,因为P﹣ABC是正三棱锥,所以P在底面的射影是底面的中心,所以PB⊥AC,因为AM∩AC=A,所以PB⊥面PAC,因为P﹣ABC是正三棱锥,所以必有PC⊥面PAB,所以PC与平面PAB所成角的大小为 ![]() ,所以②正确.
,所以②正确.
③因为因为P﹣ABC是正三棱锥,所以P在底面的射影是底面的中心,所以PA⊥BC.所以过点M与异面直线PA和BC都成 ![]() 的直线有两条,所以③错误.
的直线有两条,所以③错误.
④若二面角B﹣PA﹣C大小为 ![]() ,则∠BDC=
,则∠BDC= ![]() ,此时∠EDC=
,此时∠EDC= ![]() ,(其中E是BC的中点),
,(其中E是BC的中点), ![]() ,所以此时直线BC与平面PAC和平面PAB都成
,所以此时直线BC与平面PAC和平面PAB都成 ![]() ,又因为平面PAC和平面PAB的法向量的夹角为
,又因为平面PAC和平面PAB的法向量的夹角为 ![]() ,此时适当调整过N的直线,可以得到两条直线使得过点N与平面PAC和平面PAB都成
,此时适当调整过N的直线,可以得到两条直线使得过点N与平面PAC和平面PAB都成 ![]() ,所以满足过点N与平面PAC和平面PAB都成
,所以满足过点N与平面PAC和平面PAB都成 ![]() 的直线有3条. 所以④正确.
的直线有3条. 所以④正确.
所以答案是:①②④.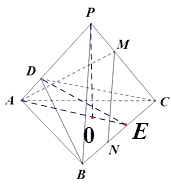

练习册系列答案
相关题目