题目内容
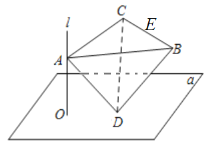
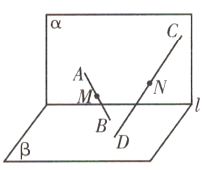
【题目】将边长为5的菱形ABCD沿对角线AC折起,顶点B移动至![]() 处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
A.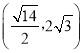 B.
B. C.
C.![]() D.
D.![]()
【答案】B
【解析】
由题意画出图形,可证AC⊥平面B′ED,得到球心O位于平面B′ED与平面ACF的交线上,即直线EF上,由勾股定理结合OA=OB′,OE<EF,EF<EB′=4可得线段EF长度的取值范围.
如图所示:

由已知可得,AC⊥B′E,且AC⊥DE,
∴AC⊥平面B′ED,
∵E是AC的中点,
∴到点A、C的距离相等的点位于平面ACF内,
同理可知,到点B′、D的距离相等的点位于平面ACF内,
∵球心O到点A,B′,C,D的距离相等,
∴球心O位于平面B′ED与平面ACF的交线上,即直线EF上.
∴球心O落在线段EF上(不含端点E、F),
显然EF⊥B′D,由题意EA=3,EB′=4,则OA2=OE2+9,
且OB′2=OF2+FB′2=OF2+EB′2﹣EF2=(EF﹣OE)2+16﹣EF2=OE2+16﹣2EFOE.
∵OA=OB′,
∴OE2+9=OE2+16﹣2EFOE,则![]() ,
,
显然OE<EF,
∴![]() EF,即EF
EF,即EF![]() .
.
又EF<EB′=4,∴![]() EF<4.
EF<4.
故选:B.

练习册系列答案
相关题目