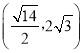题目内容
【题目】已知项数为![]() 的数列
的数列![]() 满足条件:①
满足条件:①![]() ;②
;②![]() ;若数列
;若数列![]() 满足
满足![]() ,则称
,则称![]() 为数列
为数列![]() 的“关联数列.
的“关联数列.
(1)数列1,5,9,13,17是否存在“关联数列”?若存在,写出其“关联数列”,若不存在,请说明理由;
(2)若数列![]() 存在“关联数列”
存在“关联数列”![]() ,证明:
,证明:![]() ;
;
(3)已知数列![]() 存在“关联数列”
存在“关联数列”![]() ,且
,且![]() ,
,![]() ,求数列
,求数列![]() 项数m的最小值与最大值.
项数m的最小值与最大值.
【答案】(1)存在关联数列:![]() ,10,9,8,7,理由见详解;(2)证明见详解;(3)m的最小值与最大值分别为
,10,9,8,7,理由见详解;(2)证明见详解;(3)m的最小值与最大值分别为![]() 和
和![]() .
.
【解析】
(1)根据“关联数列”定义求解判断.
(2)根据“关联数列”定义结合数列的单调性讨论即可.
(3)根据数列![]() 和求“关联数列”
和求“关联数列”![]() 的项的特征结合单调性分析出
的项的特征结合单调性分析出![]() ,根据
,根据![]() 求解.
求解.
(1)因为![]() ,
,
![]()
所以数列1,5,9,13,17存在“关联数列”![]() ,10,9,8,7.
,10,9,8,7.
(2)因为数列![]() 存在“关联数列”
存在“关联数列”![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() 为递减数列,
为递减数列,
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ;
;
(3)因为数列![]() 存在“关联数列”
存在“关联数列”![]() ,
,
所以任意![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() ,
,
![]() ,
,
由(2)知![]() ,
,
又![]() ,
,
所以![]() ,
,
解得![]() ,因为
,因为![]() ,
,
所以![]() ,
,
所以m的最小值与最大值分别为![]() 和
和![]() .
.

练习册系列答案
相关题目