题目内容
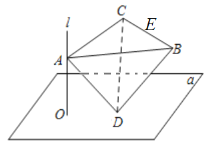
【题目】如图，直线
平面
，垂足为
，正四面体
的棱长为2，
，
分别是直线
和平面上的动点，且
，则下列判断：①点到棱
中点
的距离的最大值为
；②正四面体在平面上的射影面积的最大值为
．其中正确的说法是（ ）．
A.①②都正确B.①②都错误C.①正确，②错误D.①错误，②正确
【答案】C
【解析】
由题意，点
在以
为直径的球面上的点，所以点到棱
中点
的距离的最大值为点到球心的距离再加上球的半径，可判断①，当当
与重合时，求出正四面体
在在平面
上的射影面积，可判断②.
由题意，点在以为直径的球面上的点.
点到棱中点的距离，即以为直径的球面上的点到棱中点的距离.
所以点到棱中点的距离的最大值为点到球心的距离再加上球的半径.
设的中点为
，则为以为直径的球的球心，半径为
所以
所以点到棱中点的距离的最大值为
，故正确①.
由直线
平面，且
，则
平面.
在正四面体中，
,又，所以
平面
所以在平面上的射影
与平行且相等.
当与重合时，正四面体在在平面上的射影为对角线为2的正方形.
此时射影的面积为2，所以②不正确.
故选：C
练习册系列答案
相关题目
