题目内容
(10分)在四棱锥P—ABCD中,底面ABCD是a的正方形,PA⊥平面ABCD,
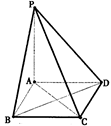
且PA=2AB
(1)求证:平面PAC⊥平面PBD;
(2)求二面角B—PC—D的余弦值.

且PA=2AB
(1)求证:平面PAC⊥平面PBD;
(2)求二面角B—PC—D的余弦值.
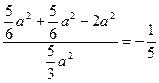
解:(Ⅰ)证明:∵PA⊥平面ABCD ∴PA⊥BD
∵ABCD为正方形 ∴AC⊥BD
∴BD⊥平面PAC又BD在平面BPD内,
∴平面PAC⊥平面BPD 6分
(Ⅱ)解法一:在平面BCP内作BN⊥PC垂足为N,连DN,
∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC;
∴∠BND为二面角B—PC—D的平面角,
在△BND中,BN=DN=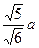 ,BD=
,BD=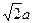
∴cos∠BND =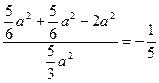
∵ABCD为正方形 ∴AC⊥BD
∴BD⊥平面PAC又BD在平面BPD内,
∴平面PAC⊥平面BPD 6分
(Ⅱ)解法一:在平面BCP内作BN⊥PC垂足为N,连DN,
∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC;
∴∠BND为二面角B—PC—D的平面角,
在△BND中,BN=DN=
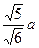 ,BD=
,BD=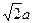
∴cos∠BND =
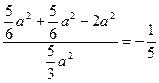

练习册系列答案
相关题目
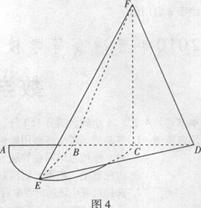
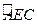 是半径为
是半径为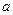 的半圆,
的半圆,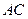 为直径,点
为直径,点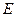 为
为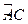 的中点,点
的中点,点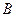 和点
和点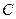 为线段
为线段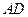 的三等分点,平面
的三等分点,平面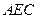 外一点
外一点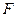 满足
满足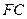
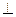 平面
平面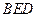 ,
,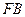 =
=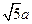 .
. 
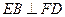 ;
; 的距离.
的距离.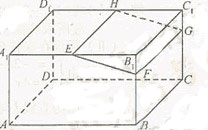
 ,
,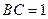 ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为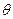 ,且
,且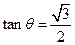 ,
,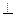 平面ABC.
平面ABC.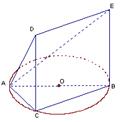
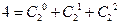 ,
,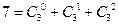 ,
,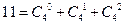 ;……
;……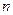 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分(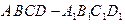 中,底面是边长为
中,底面是边长为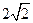 的正方形,侧棱长为4。
的正方形,侧棱长为4。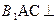 平面
平面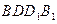 ;
;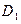 到平面
到平面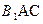 的距离d;
的距离d;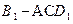 的体积V。
的体积V。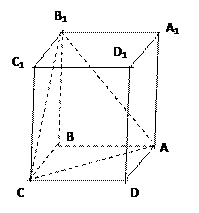
 、
、 、
、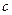 表示三条不同的直线,
表示三条不同的直线,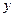 表示平面,给出下列命题:
表示平面,给出下列命题: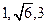 ,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。
,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。