题目内容
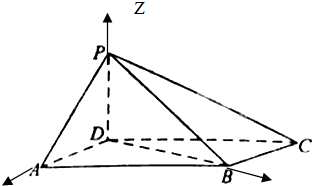
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.PD=AD
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.PD=AD(1)求二面角A-PB-C的余弦值;
(2)求点D到平面PAB的距离.
考点:二面角的平面角及求法,点、线、面间的距离计算
专题:综合题,空间位置关系与距离,空间角
分析:(1)令AD=1,则AB=2因为∠DAB=60°,AB=2AD,由余弦定理得BD=
,可得∠ADB=90°,建立空间直角坐标系,写出点A,B,C,P的坐标,求平面PAB的法向量,平面PBC的法向量,求出这两个向量的夹角的余弦值即可;
(2)由(1)知平面PAB的法向量为
=(
,1,
),利用距离公式,即可求点D到平面PAB的距离.
| 3 |
(2)由(1)知平面PAB的法向量为
| n1 |
| 3 |
| 3 |
解答:
 解:(1)令AD=1,则AB=2.
解:(1)令AD=1,则AB=2.
又∠DAB=60°,由余弦定理知BD=
=
所以AD2+BD2=AB2,即∠ADB=90°
建立如图坐标系
则A(1,0,0)、P(0,0,1)、B(0,
,0)、C(-1,
,0)
设平面PAB的法向量为
=(x,y,z),
∵
=(1,0,-1),
=(0,
,-1),
∴
,∴取
=(
,1,
)
同理平面PCB的法向量为
=(0,1,
)
cos<
,
>=
=
记二面角A-PB-C的夹角为α,如图可知α为钝角
∴cosα=-
,
故二面角A-PB-C的余弦值为-
;
(2)由(1)知平面PAB的法向量为
=(
,1,
)
∴
=(
,
,
)
又D(0,0,0),∴
=(0,0,1)
∴D到平面PAB的距离d=|
•
|=
=
 解:(1)令AD=1,则AB=2.
解:(1)令AD=1,则AB=2.又∠DAB=60°,由余弦定理知BD=
1+4-2×1×2×
|
| 3 |
所以AD2+BD2=AB2,即∠ADB=90°
建立如图坐标系
则A(1,0,0)、P(0,0,1)、B(0,
| 3 |
| 3 |
设平面PAB的法向量为
| n1 |
∵
| PA |
| PB |
| 3 |
∴
|
| n1 |
| 3 |
| 3 |
同理平面PCB的法向量为
| n2 |
| 3 |
cos<
| n1 |
| n2 |
| 1+3 | ||
2
|
2
| ||
| 7 |
记二面角A-PB-C的夹角为α,如图可知α为钝角
∴cosα=-
2
| ||
| 7 |
故二面角A-PB-C的余弦值为-
2
| ||
| 7 |
(2)由(1)知平面PAB的法向量为
| n1 |
| 3 |
| 3 |
∴
| n0 |
| ||
|
| 1 | ||
|
| ||
|
又D(0,0,0),∴
| DP |
∴D到平面PAB的距离d=|
| DP |
| n0 |
| ||
|
| ||
| 7 |
点评:此题是个中档题.考查线面垂直的性质定理和判定定理,以及应用空间向量求空间角问题,考查同学们观察、推理以及创造性地分析问题、解决问题能力.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
若A={y|y=2x,x∈R},B{(x,y)|y=x2,x∈R},则A∩B的子集个数为( )
| A、4 | B、2 | C、1 | D、0 |
若偶函数f(x)在(0,+∞)上单调递增,则不等式f(x2-3)<f(2x)的解集为( )
| A、(1,3) |
| B、(-3,-1) |
| C、(-3,-1)∪(1,3) |
| D、(-1,1)∪(3,+∞) |