题目内容
9.已知向量$\overrightarrow{OA}$⊥$\overrightarrow{AB}$,|$\overrightarrow{OA}$|=3,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=9.分析 由已知结合平面向量是数量积运算求得答案.
解答 解:由$\overrightarrow{OA}$⊥$\overrightarrow{AB}$,得$\overrightarrow{OA}$•$\overrightarrow{AB}$=0,即$\overrightarrow{OA}$•($\overrightarrow{OB}-\overrightarrow{OA}$)=0,
∵|$\overrightarrow{OA}$|=3,
∴$\overrightarrow{OA}•\overrightarrow{OB}=|\overrightarrow{OA}{|}^{2}=9$.
故答案为:9.
点评 本题考查了平面向量的数量积运算,考查了向量模的求法,是基础的计算题.

练习册系列答案
相关题目
19.设实数x,y满足$\left\{\begin{array}{l}2x+y≤10\\ x+2y≤14\\ x+y≥6\end{array}\right.$,则xy的最大值为( )
| A. | $\frac{25}{2}$ | B. | $\frac{49}{2}$ | C. | 12 | D. | 16 |
20.若集合A={i,i2,i3,i4}(i是虚数单位),B={1,-1},则A∩B等于( )
| A. | {-1} | B. | {1} | C. | {1,-1} | D. | ∅ |
4.已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )
| A. | 212 | B. | 211 | C. | 210 | D. | 29 |
14.某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(1)求Z的分布列和均值;
(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
| W | 12 | 15 | 18 |
| P | 0.3 | 0.5 | 0.2 |
(1)求Z的分布列和均值;
(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
1.已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | c<b<a |
18.设实数a,b,t满足|a+1|=|sinb|=t.则( )
| A. | 若t确定,则b2唯一确定 | B. | 若t确定,则a2+2a唯一确定 | ||
| C. | 若t确定,则sin$\frac{b}{2}$唯一确定 | D. | 若t确定,则a2+a唯一确定 |
9.过点A(-2,3)作抛物线y2=4x的两条切线l1、l2,设l1、l2与y轴分别交于点B、C,则△ABC的外接圆方程为( )
| A. | x2+y2-3x-4=0 | B. | x2+y2-2x-3y+1=0 | C. | x2+y2+x-3y-2=0 | D. | x2+y2-3x-2y+1=0 |
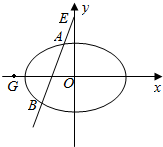 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)过点$(0,\sqrt{2})$,且离心率e为$\frac{{\sqrt{2}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)过点$(0,\sqrt{2})$,且离心率e为$\frac{{\sqrt{2}}}{2}$.