题目内容
17. 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)过点$(0,\sqrt{2})$,且离心率e为$\frac{{\sqrt{2}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)过点$(0,\sqrt{2})$,且离心率e为$\frac{{\sqrt{2}}}{2}$.(1)求椭圆E的方程;
(2)设直线x=my-1(m∈R)交椭圆E于A,B两点,判断点G$(-\frac{9}{4},0)$与以线段AB为直径的圆的位置关系,并说明理由.
分析 解法一:(1)由已知得$\left\{\begin{array}{l}{b=\sqrt{2}}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得即可得出椭圆E的方程.
(2)设点A(x1,y1),B(x2,y2),AB中点为H(x0,y0).直线方程与椭圆方程联立化为(m2+2)y2-2my-3=0,利用根与系数的关系中点坐标公式可得:y0=$\frac{m}{{m}^{2}+2}$.|GH|2=$({x}_{0}+\frac{9}{4})^{2}+{y}_{0}^{2}$.$\frac{|AB{|}^{2}}{4}$=$\frac{({m}^{2}+1)[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}{4}$,作差|GH|2-$\frac{|AB{|}^{2}}{4}$即可判断出.
解法二:(1)同解法一.
(2)设点A(x1,y1),B(x2,y2),则$\overrightarrow{GA}$=$({x}_{1}+\frac{9}{4},{y}_{1})$,$\overrightarrow{GB}$=$({x}_{2}+\frac{9}{4},{y}_{2})$.直线方程与椭圆方程联立化为(m2+2)y2-2my-3=0,计算$\overrightarrow{GA}•\overrightarrow{GB}$=$({x}_{1}+\frac{9}{4})({x}_{2}+\frac{9}{4})+{y}_{1}{y}_{2}$即可得出∠AGB,进而判断出位置关系.
解答 解法一:(1)由已知得$\left\{\begin{array}{l}{b=\sqrt{2}}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=c=\sqrt{2}}\end{array}\right.$,
∴椭圆E的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
(2)设点A(x1y1),B(x2,y2),AB中点为H(x0,y0).
由$\left\{\begin{array}{l}{x=my-1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,化为(m2+2)y2-2my-3=0,
∴y1+y2=$\frac{2m}{{m}^{2}+2}$,y1y2=$\frac{-3}{{m}^{2}+2}$,∴y0=$\frac{m}{{m}^{2}+2}$.
G$(-\frac{9}{4},0)$,
∴|GH|2=$({x}_{0}+\frac{9}{4})^{2}+{y}_{0}^{2}$=$(m{y}_{0}+\frac{5}{4})^{2}$+${y}_{0}^{2}$=$({m}^{2}+1){y}_{0}^{2}$+$\frac{5}{2}m{y}_{0}$+$\frac{25}{16}$.
$\frac{|AB{|}^{2}}{4}$=$\frac{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}{4}$=$\frac{({m}^{2}+1)[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}{4}$=$({m}^{2}+1)({y}_{0}^{2}-{y}_{1}{y}_{2})$,
故|GH|2-$\frac{|AB{|}^{2}}{4}$=$\frac{5}{2}m{y}_{0}+({m}^{2}+1){y}_{1}{y}_{2}$+$\frac{25}{16}$=$\frac{5{m}^{2}}{2({m}^{2}+2)}$-$\frac{3({m}^{2}+1)}{{m}^{2}+2}$+$\frac{25}{16}$=$\frac{17{m}^{2}+2}{16({m}^{2}+2)}$>0.
∴$|GH|>\frac{|AB|}{2}$,故G在以AB为直径的圆外.
解法二:(1)同解法一.
(2)设点A(x1y1),B(x2,y2),则$\overrightarrow{GA}$=$({x}_{1}+\frac{9}{4},{y}_{1})$,$\overrightarrow{GB}$=$({x}_{2}+\frac{9}{4},{y}_{2})$.
由$\left\{\begin{array}{l}{x=my-1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,化为(m2+2)y2-2my-3=0,
∴y1+y2=$\frac{2m}{{m}^{2}+2}$,y1y2=$\frac{-3}{{m}^{2}+2}$,
从而$\overrightarrow{GA}•\overrightarrow{GB}$=$({x}_{1}+\frac{9}{4})({x}_{2}+\frac{9}{4})+{y}_{1}{y}_{2}$
=$(m{y}_{1}+\frac{5}{4})(m{y}_{2}+\frac{5}{4})$+y1y2
=$({m}^{2}+1){y}_{1}{y}_{2}+\frac{5}{4}m({y}_{1}+{y}_{2})$+$\frac{25}{16}$
=$\frac{5{m}^{2}}{2({m}^{2}+2)}$-$\frac{3({m}^{2}+1)}{{m}^{2}+2}$+$\frac{25}{16}$=$\frac{17{m}^{2}+2}{16({m}^{2}+2)}$>0.
∴$\overrightarrow{GA}•\overrightarrow{GB}$>0,又$\overrightarrow{GA}$,$\overrightarrow{GB}$不共线,
∴∠AGB为锐角.
故点G$(-\frac{9}{4},0)$在以AB为直径的圆外.
点评 本小题主要考查椭圆、圆、直线与椭圆的位置关系、点与圆的位置关系、向量数量积运算性质等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想,属于难题.

| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
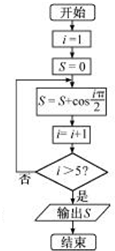
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
| A. | ($\frac{5}{4}$,$\frac{7}{4}$] | B. | ($\frac{3}{4}$,$\frac{4}{5}$] | C. | (1,$\frac{5}{4}$] | D. | ($\frac{3}{4}$,$\frac{5}{4}$] |
 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,若在矩形ABCD 内随机取一点,则此点取自阴影部分的概率等于$\frac{5}{12}$.
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,若在矩形ABCD 内随机取一点,则此点取自阴影部分的概率等于$\frac{5}{12}$.