题目内容
【题目】对于函数f(x)(x∈D)，若x∈D时，均有f′(x)<f(x)成立，则称函数f(x)是J函数．
(Ⅰ)当函数f(x)＝x2＋m(ex＋x)，x≥e是J函数时，求实数m的取值范围；
(Ⅱ)若函数g(x)为R＋上的J函数，试比较g(a)与ea－1g(1)的大小．
【答案】(Ⅰ)m>
(Ⅱ)见解析
【解析】试题分析：（1）根据J函数的定义，解不等式f'（x）>f（x），通过这个不等式，我们可以求出m的取值范围，
（2）根据函数g（x）为（0，+∞）上的J函数，构造函数h(x)＝
，利用函数的单调性进行判断．
试题解析：(Ⅰ)由f(x)＝x2＋m(ex＋x)，x≥e得f′(x)＝2x＋m(ex＋1)，x≥e，
由f′(x)<f(x)得2x＋m(ex＋1)<x2＋m(ex＋x)，
∴m(x－1)>2x－x2，又x≥e，∴m>
，
令y＝
，则y′＝
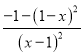<0，
又x≥e，∴ymax＝
，∴m>
.
(Ⅱ)构造函数h(x)＝
，x∈R＋，
则h′(x)＝
<0，可得h(x)为R＋上的减函数．
当a>1时，h(a)<h(1)，
即
，得g(a)<ea－1g(1)；
当0<a<1时，h(a)>h(1)，即
，
得g(a)>ea－1g(1)；
当a＝1时，h(a)＝h(1)，即
，得g(a)＝ea－1g(1).
黄冈冠军课课练系列答案【题目】为了响应我市“创建宜居港城，建设美丽莆田”，某环保部门开展以“关爱木兰溪，保护母亲河”为主题的环保宣传活动，将木兰溪流经市区河段分成
段，并组织青年干部职工对每一段的南、北两岸进行环保综合测评，得到分值数据如下表：
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
（Ⅰ）记评分在
以上（包括）为优良，从中任取一段，求在同一段中两岸环保评分均为优良的概率；
（Ⅱ）根据表中数据完成下面茎叶图；
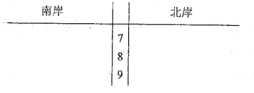
（Ⅲ）分别估计两岸分值的中位数，并计算它们的平均值，试从计算结果分析两岸环保情况，哪边保护更好.
