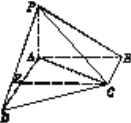
题目内容
【题目】如图,平面五边形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=![]() ,cos∠EDC=
,cos∠EDC=![]() .将△CDE沿CE折起,使点D移动到P的位置,且AP=
.将△CDE沿CE折起,使点D移动到P的位置,且AP=![]() ,得到四棱锥P-ABCE.
,得到四棱锥P-ABCE.
(1)求证:AP⊥平面ABCE;
(2)记平面PAB与平面PCE相交于直线l,求证:AB∥l.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)在![]() 中,由已知结合余弦定理得
中,由已知结合余弦定理得![]() ,连接
,连接![]() ,可得
,可得![]() ,在
,在![]() 中,由
中,由![]() ,得
,得![]() ,同理
,同理![]() ,然后利用线面垂直的判定可得
,然后利用线面垂直的判定可得![]() 平面
平面![]() ;
;
(2)由![]() ,且
,且![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,又平面
,又平面![]() 平面
平面![]() ,结合面面平行的性质可得
,结合面面平行的性质可得![]() .
.
试题解析:
(1)在△CDE中,
∵CD=ED=![]() ,cos∠EDC=
,cos∠EDC=![]() ,
,
由余弦定理,CE2=(![]() )2+(
)2+(![]() )2-2×
)2-2×![]() ×
×![]() ×
×![]() =4,
=4,
∴CE=2.连接AC,
∵AE=2,∠AEC=60°,∴AC=2.
又∵AP=![]() ,
,
∴在△PAE中,PA2+AE2=PE2,即AP⊥AE,同理AP⊥AC,而AC,AE平面ABCE,AC∩AE=A,
故AP⊥平面ABCE.
(2)∵AB∥CE,且CE平面PCE,AB平面PCE,
∴AB∥平面PCE.
又平面PAB∩平面PCE=l,∴AB∥l.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目