题目内容
【题目】已知函数![]() ,若函数
,若函数![]() 有6个不同的零点,则实数m的取值范围是__________.
有6个不同的零点,则实数m的取值范围是__________.
【答案】m<﹣3
【解析】
令t=f(x),则原函数y等价为y=2t2+3mt+1﹣2m,转化为一元二次函数和二次方程问题,结合函数f(x)的图象,讨论t的范围,从而确定m的取值范围.
令t=f(x),则原函数等价为y=2t2+3mt+1﹣2m,
作出函数f(x)的图象如图,
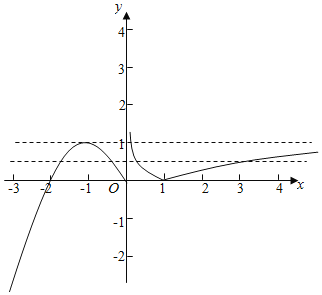
图象可知:
当t<0时,函数t=f(x)有一个零点;
当t=0时,函数t=f(x)有三个零点;
当0<t<1时,函数t=f(x)有四个零点;
当t=1时,函数t=f(x)有三个零点;
当t>1时,函数t=f(x)有两个零点.
要使关于x的函数y=2f2(x)+3mf(x)+1﹣2m有6个不同的零点,
则方程2t2+3mt+1﹣2m=0有两个根t1,t2,
且0<t1<1,t2>1或t1=0,t2=1,
令g(t)=2t2+3mt+1﹣2m,则由根的分布可得,
将t=1,代入g(t)=0得m=﹣3,
此时2t2﹣9t+7=0的另一个根为t=![]() ,不满足t1=0,t2=1,
,不满足t1=0,t2=1,
若0<t1<1,t2>1,则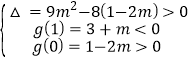
即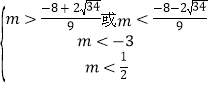
解得m<﹣3,
故答案为:m<﹣3

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目