题目内容
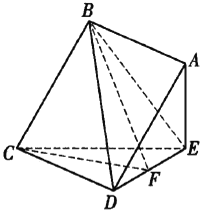
【题目】如图,已知![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .若四边形
.若四边形![]() 为矩形,线段
为矩形,线段![]() 与
与![]() 交于点
交于点![]() .
.

(1)证明:![]() ∥平面
∥平面![]() .
.
(2)求二面角![]() 的大小。
的大小。
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,请求出
?若存在,请求出![]() 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
【答案】(1)详见解析;(2)![]() (3)在线段
(3)在线段![]() 上存在一点
上存在一点![]() ,且
,且![]()
【解析】
试题(1)连接![]() 在
在![]() 中,由题设知
中,由题设知![]() 分别为
分别为![]() 中点,所以
中点,所以![]() 由此可证
由此可证![]() // 平面
// 平面![]() ;
;
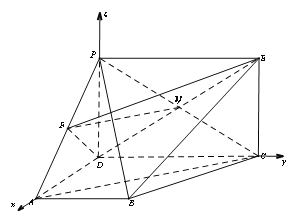
(2)如图以![]() 为原点,分别以
为原点,分别以![]() 所在直线为x,y,z轴,建立空间直角坐标系
所在直线为x,y,z轴,建立空间直角坐标系![]() 利用空间向量的数量积求出平面ABC和平面PBC的法向量的坐标,由法向量的夹角公式求出求二面角
利用空间向量的数量积求出平面ABC和平面PBC的法向量的坐标,由法向量的夹角公式求出求二面角![]() 的大小;
的大小;
(3)首先假设存在点Q满足条件.由![]() 设
设![]() ,再利用向量的夹角公式确定
,再利用向量的夹角公式确定![]() 的值.
的值.
试题解析:解:(Ⅰ)连接![]() 在
在![]() 中,
中,![]() 分别为
分别为![]() 中点,所以
中点,所以![]()
因为![]()
所以![]() 4分
4分
(2)如图以![]() 为原点,分别以
为原点,分别以![]() 所在直线为x,y,z轴,建立空间直角坐标系
所在直线为x,y,z轴,建立空间直角坐标系![]() 5分
5分
则![]()
设平面![]() 的法向量为
的法向量为![]() 则
则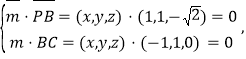
即![]() 解得
解得![]()
令![]() ,得
,得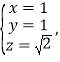 所以
所以![]() 7分
7分
因为平![]()
所以![]() ,
,
由图可知二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的大小为
的大小为![]() 9分
9分
(3)设存在点Q满足条件.
由![]() 设
设![]() ,
,
整理得![]() ,
,![]() 11分
11分
因为直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,
,
所以![]() , 13分
, 13分
则![]() 知
知![]() ,即
,即![]() 点与E点重合.
点与E点重合.
故在线段![]() 上存在一点
上存在一点![]() ,且
,且![]() 14分
14分

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目