题目内容
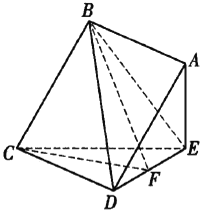
【题目】如图，把等腰直角三角形
沿斜边
所在直线旋转至
的位置，使
.
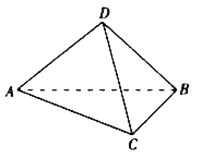
(1)求证:平面
平面；
(2)求二面角
的余弦值.
【答案】(1)证明见解析(2) 
【解析】
（1）取
的中点
，连接
，可得得
，根据三角形中的几何关系，得到
，从而得到
，所以得到
平面
，再得到平面
平面；（2）取
的中点
，连接
，
，再在直角三角形
中，得到
，从而得到二面角
的余弦值.
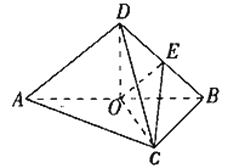
（1）如图，取的中点，连接
，
是等腰直角三角形， 
，且
.
连接，同理得，且
，
，
.
，
，
为等腰直角三角形，，
又
，
平面，
平面.
又
平面
，
∴平面平面.
（2）取的中点，连接.
易知
为等边三角形， .
又
为等腰直角三角形，.
为二面角的平面角.
由（1）知，，
且
平面，
，
所以
平面，
平面，
.
为直角三角形.
设
，则
，
所以
，
则
，
，
即二面角的余弦值为.
阅读快车系列答案【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关，随机抽取了30名男性和30名女性观众，抽查结果用等高条形图表示如图：
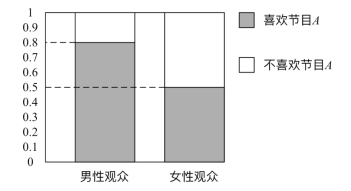
根据该等高条形图，完成下列2×2列联表，并用独立性检验的方法分析，能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关？
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 | 60 |
附：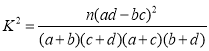
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某企业生产某种产品，为了提高生产效益，通过引进先进的生产技术和管理方式进行改革，并对改革后该产品的产量x（万件）与原材料消耗量y（吨）及100件产品中合格品与不合格品数量作了记录，以便和改革前作对照分析，以下是记录的数据：
表一：改革后产品的产量和相应的原材料消耗量
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
表二：改革前后定期抽查产品的合格数与不合格数
合格品的数量 | 不合格品的数量 | 合计 | |
改革前 | 90 | 10 | 100 |
改革后 | 85 | 15 | 100 |
合计 | 175 | 25 | 200 |
（1）请根据表一提供数据，用最小二乘法求出y关于x的线性回归方程
.
（2）已知改革前生产7万件产品需要6.5吨原材料，根据回归方程预测生产7万件产品能够节省多少原材料？
（3）请根据表二提供的数据，判断是否有90%的把握认为“改革前后生产的产品的合格率有差异”？
