题目内容
【题目】从集合
中删去
个数，使得剩下的元素中，任两个数之和均不为2015的因数。求的最小值。
【答案】见解析
【解析】
注意到，集合
中任两个元素之和不大于71.
由于2015=5×13×31不大于71的正因数有1、5、13、31、65，
故在集合的二元子集中，
元素和为5的有
，
；
元素和为13的有
，
，
，
，
，
，…，
；
元素和为65的有
，
，
，
.
为直观起见，将其画成一个图，每条线段两端的数为上述一个二元子集，如图所示.
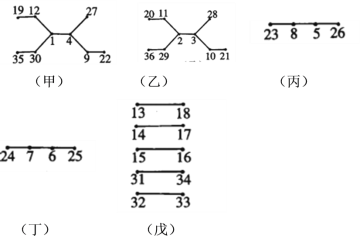
为了不构成这些和，每对数（每条线段）中至少要删去一个数.
于是，在图中（甲）、（乙）中各至少要删去四个数，图中（丙）、（丁）中各至少要删去两个数，图中（戊）中至少要删去五个数，总共至少要删去17个数.
另一方便，删去适当的17个数，可以使得余下的数满足条件.例如，在图中（甲）中删去12、30、4、22，图中（乙）中删去11、29、3、21，图中（丙）中删去23、5，图中（丁）中删去24、6，图中（戊）中删去13、14、15、31、32.此时，图中所有的线段均已被断开.
练习册系列答案
相关题目
