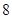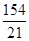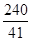题目内容
已知数列{an}的前n项和为Sn,且对任意n∈N*有an+Sn=n.
(1)设bn=an-1,求证:数列{bn}是等比数列;
(2)设c1=a1且cn=an-an-1 (n≥2),求{cn}的通项公式.
(1)设bn=an-1,求证:数列{bn}是等比数列;
(2)设c1=a1且cn=an-an-1 (n≥2),求{cn}的通项公式.
(1)证明见解析(2)cn= ( )n
)n
 )n
)n(1)证明 由a1+S1=1及a1=S1得a1= .
.
又由an+Sn=n及an+1+Sn+1=n+1得
an+1-an+an+1=1,∴2an+1=an+1.
∴2(an+1-1)=an-1,即2bn+1=bn.
∴数列{bn}是以b1=a1-1=- 为首项,
为首项,
 为公比的等比数列. 6分
为公比的等比数列. 6分
(2)解 方法一 由(1)知2an+1=an+1.
∴2an=an-1+1 (n≥2), 8分
∴2an+1-2an=an-an-1,
∴2cn+1=cn (n≥2).
又c1=a1= ,a2+a1+a2=2,∴a2=
,a2+a1+a2=2,∴a2= .
.
∴c2= -
- =
= ,即c2=
,即c2= c1.
c1.
∴数列{cn}是首项为 ,公比为
,公比为 的等比数列. 12分
的等比数列. 12分
∴cn= ·(
·( )n-1=(
)n-1=( )n. 14分
)n. 14分
方法二 由(1)bn=(- )·(
)·( )n-1=-(
)n-1=-( )n.
)n.
∴an=-( )n+1.
)n+1.
∴cn=-( )
) +1-
+1-
= -
- =
=

= (n≥2). 12分
(n≥2). 12分
又c1=a1= 也适合上式,∴cn=
也适合上式,∴cn= . 14分
. 14分
 .
.又由an+Sn=n及an+1+Sn+1=n+1得
an+1-an+an+1=1,∴2an+1=an+1.
∴2(an+1-1)=an-1,即2bn+1=bn.
∴数列{bn}是以b1=a1-1=-
 为首项,
为首项, 为公比的等比数列. 6分
为公比的等比数列. 6分(2)解 方法一 由(1)知2an+1=an+1.
∴2an=an-1+1 (n≥2), 8分
∴2an+1-2an=an-an-1,
∴2cn+1=cn (n≥2).
又c1=a1=
 ,a2+a1+a2=2,∴a2=
,a2+a1+a2=2,∴a2= .
.∴c2=
 -
- =
= ,即c2=
,即c2= c1.
c1.∴数列{cn}是首项为
 ,公比为
,公比为 的等比数列. 12分
的等比数列. 12分∴cn=
 ·(
·( )n-1=(
)n-1=( )n. 14分
)n. 14分方法二 由(1)bn=(-
 )·(
)·( )n-1=-(
)n-1=-( )n.
)n.∴an=-(
 )n+1.
)n+1.∴cn=-(
 )
) +1-
+1-
=
 -
- =
=

=
 (n≥2). 12分
(n≥2). 12分又c1=a1=
 也适合上式,∴cn=
也适合上式,∴cn= . 14分
. 14分
练习册系列答案
相关题目
 (an-1).
(an-1).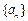 中,
中, ,
,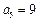 ;数列
;数列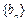 的前
的前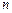 项和是
项和是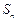 ,且
,且 .
.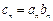 ,求
,求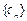 的前n项和
的前n项和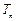 .
.
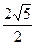
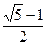

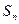 为等比数列
为等比数列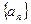 前
前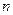 项和,
项和,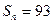 ,
,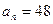 ,公比
,公比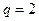 ,则项数
,则项数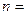 .
.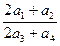 的值为 ( )
的值为 ( )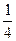
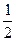
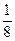
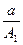 +
+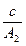 的值等于( )
的值等于( )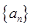 中,若
中,若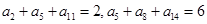 ,
, 的值为( )
的值为( )