题目内容
等差数列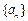 中,
中, ,
,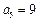 ;数列
;数列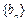 的前
的前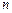 项和是
项和是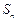 ,且
,且 .
.
(Ⅰ) 求数列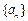 的通项公式;
的通项公式;
(Ⅱ) 求证:数列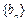 是等比数列;
是等比数列;
(Ⅲ) 记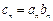 ,求
,求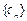 的前n项和
的前n项和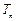 .
.
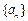 中,
中, ,
,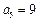 ;数列
;数列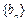 的前
的前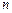 项和是
项和是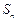 ,且
,且 .
.(Ⅰ) 求数列
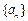 的通项公式;
的通项公式;(Ⅱ) 求证:数列
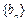 是等比数列;
是等比数列;(Ⅲ) 记
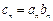 ,求
,求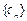 的前n项和
的前n项和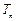 .
.(Ⅰ)
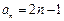 (Ⅲ)
(Ⅲ)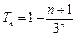
(Ⅰ)设数列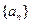 的公差为d,由
的公差为d,由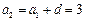 ,
,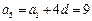 ,
,
解得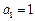 ,
,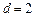 ,∴
,∴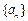 通项公式为
通项公式为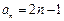 .……………………3分
.……………………3分
(Ⅱ)由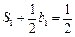 得
得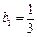 ,由
,由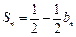 ,
,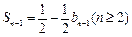 ,
,
得 ,∴
,∴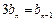 即
即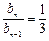 ,………5分
,………5分
∵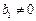 ,∴
,∴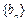 是以
是以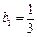 为首项,
为首项,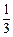 为公比的等比数列.………………7分
为公比的等比数列.………………7分
(Ⅲ)由(Ⅱ)得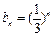 ,则
,则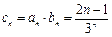 ,从而
,从而
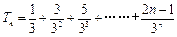 ,∴
,∴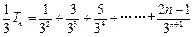 ,……………9分
,……………9分
∴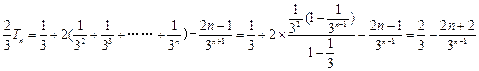 ,
,
∴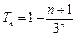 .…………………………………………12分
.…………………………………………12分
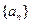 的公差为d,由
的公差为d,由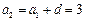 ,
,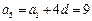 ,
, 解得
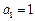 ,
,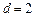 ,∴
,∴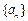 通项公式为
通项公式为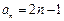 .……………………3分
.……………………3分(Ⅱ)由
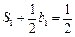 得
得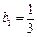 ,由
,由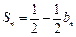 ,
,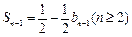 ,
,得
 ,∴
,∴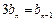 即
即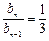 ,………5分
,………5分∵
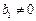 ,∴
,∴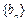 是以
是以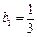 为首项,
为首项,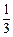 为公比的等比数列.………………7分
为公比的等比数列.………………7分(Ⅲ)由(Ⅱ)得
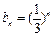 ,则
,则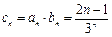 ,从而
,从而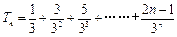 ,∴
,∴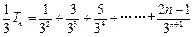 ,……………9分
,……………9分∴
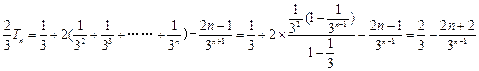 ,
,∴
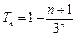 .…………………………………………12分
.…………………………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
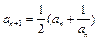 ,{bn}中
,{bn}中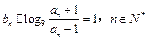 .
.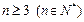 时,证明:
时,证明: .
.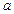 元,每期利率为
元,每期利率为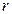 ,设本利和为
,设本利和为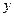 ,存期为
,存期为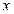 ,写出本利和
,写出本利和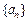 的前n项和
的前n项和 满足
满足 ,
, 为等比数列,且
为等比数列,且 ,
, ,
, ,
, ;
; ,求数列
,求数列 的前n项和
的前n项和 .
.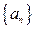 是等差数列,
是等差数列,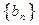 是等比数列,且
是等比数列,且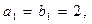
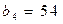 ,
, 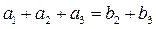 ,(I)求数列
,(I)求数列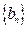 的通项公式;(II)求数列
的通项公式;(II)求数列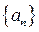 的前10项和
的前10项和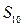
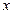 的多项式
的多项式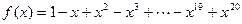 表为关于
表为关于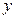 的多项式
的多项式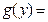
 其中
其中 则
则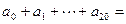 .
.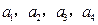 成等比数列,且
成等比数列,且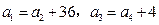 ,求
,求 的前n项和
的前n项和 ,则此数列奇数项的前n项和为
,则此数列奇数项的前n项和为


