题目内容
图2-4-1是一个计算装置示意图,J1、J2是数据入口,C是计算结果的出口,计算过程是由J1,J2分别输入自然数m和n,经过计算后得自然数k由C输出,此种计算装置完成的计算满足以下三个性质:
①若J1、J2分别输入1,则输出结果1;
②若J1输入任何固定自然数不变,J2输入自然数增大1,则输出结果比原来增大2;
③若J2输入1,J1输入自然数增大1,则输出结果为原来的2倍.
试问:(1)若J1输入1,J2输入自然数n,则输出结果为多少?
(2)若J2输入1,J1输入自然数m,则输出结果为多少?
(3)若J1输入自然数m,J2输入自然数n,则输出结果为多少?
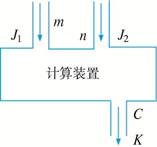
图2-4-1
①若J1、J2分别输入1,则输出结果1;
②若J1输入任何固定自然数不变,J2输入自然数增大1,则输出结果比原来增大2;
③若J2输入1,J1输入自然数增大1,则输出结果为原来的2倍.
试问:(1)若J1输入1,J2输入自然数n,则输出结果为多少?
(2)若J2输入1,J1输入自然数m,则输出结果为多少?
(3)若J1输入自然数m,J2输入自然数n,则输出结果为多少?

图2-4-1
(1)由条件①有f(1,1)=1,由条件②知f(m,n+1)=f(m,n)+2,即当m固定时,f(m,n)成等差数列.
∴f(m,n)=f(m,1)+2(n-1).
故f(1,n)=f(1,1)+2(n-1)=2n-1.
(2)由条件③知f(m+1,1)=2f(m,1),即f(m,1)是一等比数列.
∴f(m,1)=f(1,1)·2m-1=2m-1.
(3)由(1)(2)知f(m,n)=f(m,1)+2(n-1)=2m-1+2n-2.
∴f(m,n)=f(m,1)+2(n-1).
故f(1,n)=f(1,1)+2(n-1)=2n-1.
(2)由条件③知f(m+1,1)=2f(m,1),即f(m,1)是一等比数列.
∴f(m,1)=f(1,1)·2m-1=2m-1.
(3)由(1)(2)知f(m,n)=f(m,1)+2(n-1)=2m-1+2n-2.
本题信息量大,粗看不知如何入手,但若把条件写成二元函数式,并把它看作某一变量的函数,抽象出等差或等比数列模型,问题便迎刃而解.

练习册系列答案
相关题目
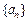 的前n项和
的前n项和 满足
满足 ,
, 为等比数列,且
为等比数列,且 ,
, ,
, ,
, ;
; ,求数列
,求数列 的前n项和
的前n项和 .
.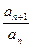 ;②bn=an·an+1;③bn=nan;④bn=an2.
;②bn=an·an+1;③bn=nan;④bn=an2.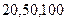 依次加上同一个常数后组成一个等比数列,则这个等比数列的公比为 .
依次加上同一个常数后组成一个等比数列,则这个等比数列的公比为 .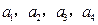 成等比数列,且
成等比数列,且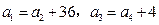 ,求
,求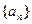 中,
中,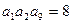 ,则
,则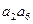 = 。
= 。