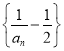题目内容
【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪70元,每单抽成3元;乙公司无底薪,40单以内(含40单)的部分每单抽成5元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到频数表如下:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
将上表中的频率视为概率,回答下列问题:
(1)现从甲公司随机抽取3名送餐员,求恰有2名送餐员送餐单数超过40的概率;
(2)(i)记乙公司送餐员日工资为X(单位:元),求X的数学期望;
(ii)某人拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日平均工资的角度考虑,他应该选择去哪家公司应聘,说明理由.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)由表格可知100天中,送餐天数超过40的有20天,根据古典概型即可求出概率;(2)计算乙公司送餐员日工资的期望值,计算甲公司的送餐员日平均工资,比较两者大小即可.
试题解析:(1)从甲公司记录的100天中随机抽取1天,送餐单数超过40的概率![]() .有放回地抽取3次,3次抽取中,恰有2次送餐单数超过40的概率是
.有放回地抽取3次,3次抽取中,恰有2次送餐单数超过40的概率是
![]() .
.
(2)(i)设乙公司送餐员送餐单数为a,乙公司送餐员日工资为X元.
当a=38时,X=38×5=190;当a=39时,X=39×5=195;当a=40时,X=40×5=200;当a=41时,X=40×5+1×7=207;当a=42时,X=40×5+2×7=214.
X的所有可能取值为190,195,200,207,214.
故X的分布列为:
X | 190 | 195 | 200 | 207 | 214 |
P |
|
|
|
|
|
X的数学期望E(X)=190×![]() +195×
+195×![]() +200×
+200×![]() +207×
+207×![]() +214×
+214×![]() =
=![]() (元).
(元).
(ii)公司送餐员日平均送餐单数为38×0.2+390.4+40×0.2+41×0.1+42×0.1=39.5.
所以甲公司送餐员日平均工资为70+3×39.5=188.5(元).
因为188.5<202.2,故这个人应该选择去乙公司应聘.

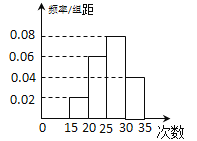
【题目】某次有600人参加的数学测试,其成绩的频数分布表如图所示,规定85分及其以上为优秀.
区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人数 | 36 | 114 | 244 | 156 | 50 |
(Ⅰ)现用分层抽样的方法从这600人中抽取20人进行成绩分析,求其中成绩为优秀的学生人数;
(Ⅱ)在(Ⅰ)中抽取的20名学生中,要随机选取2名学生参加活动,记“其中成绩为优秀的人数”为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.