题目内容
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .过
.过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.

(l)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:四边形![]() 为平行四边形;
为平行四边形;
(Ⅲ)若是![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)见解析(2) 见解析(3) ![]()
【解析】试题分析:(Ⅰ)由线面垂直的性质 可得![]() ,由菱形的性质可得
,由菱形的性质可得![]() .从而由线面垂直的判定定理可得
.从而由线面垂直的判定定理可得![]() 平面
平面![]() ;(Ⅱ)先证明
;(Ⅱ)先证明![]() 平面
平面![]() ,再根据线面平行的性质可得
,再根据线面平行的性质可得![]() ,根据面面平行的性质可得
,根据面面平行的性质可得![]() ,从而得四边形
,从而得四边形![]() 为平行四边形;(Ⅲ)在平面
为平行四边形;(Ⅲ)在平面![]() 内,过
内,过![]() 作
作![]() .因为
.因为 ![]() 平面
平面![]() ,所以,以
,所以,以![]() 为轴建立空间直角坐标系,可知平面
为轴建立空间直角坐标系,可知平面![]() 的法向量为
的法向量为![]() ,根据向量垂直数量积为零列方程组求出平面
,根据向量垂直数量积为零列方程组求出平面![]() 的法向量,利用空间向量夹角余弦公式可得结果.
的法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(Ⅰ)因为 ![]() 平面
平面![]() ,所以
,所以 ![]() .
.
因为 三棱柱![]() 中,
中, ![]() ,所以 四边形
,所以 四边形![]() 为菱形,
为菱形,
所以 ![]() .
. ![]() 与
与![]() 在平面
在平面![]() 内相交.
内相交.
所以 ![]() 平面
平面![]() .
.
(Ⅱ)因为 ![]() ,
, ![]() 平面
平面![]() ,所以
,所以 ![]() 平面
平面![]() .
.
因为 平面![]() 平面
平面![]() ,所以
,所以 ![]() .
.
因为 平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以 ![]() .
.
所以 四边形![]() 为平行四边形.
为平行四边形.
(Ⅲ)在平面![]() 内,过
内,过![]() 作
作![]() .
.
因为 ![]() 平面
平面![]() ,
,
如图建立空间直角坐标系![]() .
.
由题意得, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
因为 ![]() ,所以
,所以  ,
,
所以 ![]() .
.
由(Ⅰ)得平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则 即
即
令![]() ,则
,则![]() ,
, ![]() ,所以
,所以 ![]() .
.
所以  .
.
由图知 二面角![]() 的平面角是锐角,
的平面角是锐角,
所以 二面角![]() 的大小为
的大小为![]() .
.

【方法点晴】本题主要考查线面垂直的判定定理、线面平行的性质、面面平行的直线以及利用空间向量求二面角,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

【题目】![]() 年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从
年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从![]() 年下半年的会员中随机调查了
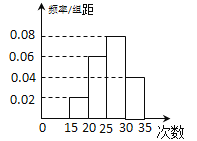
年下半年的会员中随机调查了![]() 个会员,得到会员对售后服务的满意度评分如下:
个会员,得到会员对售后服务的满意度评分如下:
![]()
根据会员满意度评分,将会员的满意度从低到高分为三个等级:
满意度评分 | 低于 |
| 不低于 |
满意度等级 | 不满意 | 比较满意 | 非常满意 |
(1)根据这![]() 个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
(2)以(1)中的频率作为概率,假设每个会员的评价结果相互独立.
(i)若从下半年的所有会员中随机选取![]() 个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
(ii)若从下半年的所有会员中随机选取![]() 个会员,记评分非常满意的会员的个数为
个会员,记评分非常满意的会员的个数为![]() ,求
,求![]() 的分布列,数学期望
的分布列,数学期望![]() 及方差
及方差![]() .
.
【题目】为了治理大气污染,某市2017年初采用了一系列措施,比如“煤改电”,“煤改气”,“国Ⅰ,Ⅱ轻型汽油车限行”,“整治散乱污染企业”等.下表是该市2016年和2017年12月份的空气质量指数(AQI)(AQI指数越小,空气质量越好)统计表.
表1:2016年12月AQI指数表:单位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 47 | 123 | 232 | 291 | 78 | 103 | 159 | 132 | 37 | 67 | 204 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 270 | 78 | 40 | 51 | 135 | 229 | 270 | 265 | 409 | 429 | 151 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 47 | 155 | 191 | 64 | 54 | 85 | 75 | 249 | 329 |
表2:2017年12月AQI指数表:单位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 91 | 187 | 79 | 28 | 44 | 49 | 27 | 41 | 56 | 43 | 28 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 28 | 49 | 94 | 62 | 40 | 46 | 48 | 55 | 44 | 74 | 62 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 50 | 50 | 46 | 41 | 101 | 140 | 221 | 157 | 55 |
根据表中数据回答下列问题:
(Ⅰ)求出2017年12月的空气质量指数的极差;
(Ⅱ)根据《环境空气质量指数(AQI)技术规定(试行)》规定:当空气质量指数为0~50时,空气质量级别为一级.从2017年12月12日到12月16这五天中,随机抽取三天,空气质量级别为一级的天数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)你认为该市2017年初开始采取的这些大气污染治理措施是否有效?结合数据说明理由.