题目内容
4.已知a∈R,f(x)=(x2-4)(x-a).(1)求f′(x);
(2)若f′(-1)=0,求函数f(x)在[-2,4]上的最大值和最小值.
分析 (1)将f(x)展开,利用导数的公式以及运算法则求导.
(2)利用f′(-1)=0求出a,得到f(x)的解析式以及导数,求出极值点,比较端点函数值与极值的大小,得到最值.
解答 解:(1)f(x)=(x2-4)(x-a)=x3-ax2-4x+4a,
所以f′(x)=(x3-ax2-4x+4a)'=3x2-2ax-4;
(2)若f′(-1)=0,则3+2a-4=0解得a=$\frac{1}{2}$,
所以f(x)=(x2-4)(x-$\frac{1}{2}$).令f'(x)=3x2-x-4=0解得x=-1,x=$\frac{4}{3}$.
f(-2)=0,f(-1)=$\frac{9}{2}$,f($\frac{4}{3}$)=$-\frac{50}{27}$,f(4)=42,
所以函数f(x)在[-2,4]上的最大值为42,最小值为$-\frac{50}{27}$.
点评 本题考查了函数求导以及函数闭区间的最值的求法.

练习册系列答案
相关题目
12.如图C是△PAB边AB内的一点,下列说法正确的是( )
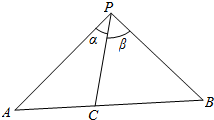

| A. | PCsin(α+β)=PBsinα+PAsinβ | B. | PCsin(α+β)=PAsinα+PBsinβ | ||
| C. | $\frac{sin(α+β)}{PC}$=$\frac{sinα}{PB}$+$\frac{sinβ}{PA}$ | D. | $\frac{sin(α+β)}{PC}$=$\frac{sinα}{PA}$+$\frac{sinβ}{PB}$ |