题目内容
已知二次函数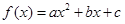 经过点
经过点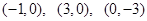
(1)求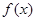 的解析式;
的解析式;
(2)当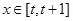 时,求
时,求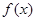 的最小值
的最小值 。
。
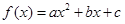 经过点
经过点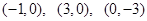
(1)求
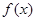 的解析式;
的解析式;(2)当
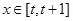 时,求
时,求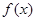 的最小值
的最小值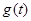 。
。解:根据题意可知二次函数与x轴的两个交点为(-1,0)(3,0)因此设f(x)=a(x+1)(x-3),且f(0)=-3,解得a=1,故函数的解析式为f(x)=x2-2x-3,。
当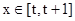 时利用定义域与对称轴的关系进行分类讨论得到结论。求解得到最小值。
时利用定义域与对称轴的关系进行分类讨论得到结论。求解得到最小值。
当
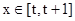 时利用定义域与对称轴的关系进行分类讨论得到结论。求解得到最小值。
时利用定义域与对称轴的关系进行分类讨论得到结论。求解得到最小值。本试题主要是考查了二次函数的解析式的求解问题,以及二次函数的最值的运用。
(1)根据已知的点的坐标,设出二次函数的两根式,然后将第三个点代入得到参数a的值。
(2)在第一问的基础上可知,函数的开口和对称轴x=1,但是定义域与对称轴的关系不确定,因此分类讨论得到结论。
(1)根据已知的点的坐标,设出二次函数的两根式,然后将第三个点代入得到参数a的值。
(2)在第一问的基础上可知,函数的开口和对称轴x=1,但是定义域与对称轴的关系不确定,因此分类讨论得到结论。

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
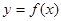 是二次函数,方程
是二次函数,方程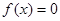 有两个相等实根,且
有两个相等实根,且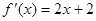 .
.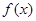 的解析式;
的解析式;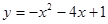 所围成图形的面积.
所围成图形的面积.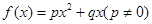 ,其导函数为
,其导函数为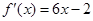 ,数列
,数列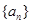 的前
的前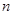 项和为
项和为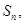 点
点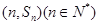 均在函数
均在函数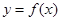 的图像上;.
的图像上;.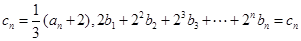 ,求数列
,求数列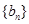 的通项公式;
的通项公式;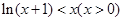 成立,
成立,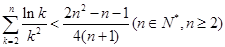
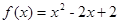 在区间
在区间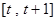
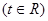 上的最小值记为
上的最小值记为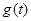

 的解集为
的解集为 ,求实数
,求实数 的取值范围;
的取值范围;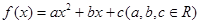 ,满足:对任意实数
,满足:对任意实数 ,都有
,都有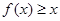 ,且当
,且当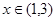 时,有
时,有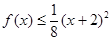 成立,又
成立,又 ,则
,则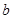 为( )
为( )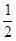
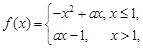 若
若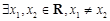 ,使得
,使得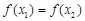 成立,则实数
成立,则实数 的取值范围是
的取值范围是 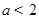
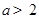
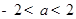
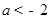
 的图像过原点,且它的导函数
的图像过原点,且它的导函数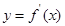 的图像是经过第一、二、三象限的一条直线,则函数
的图像是经过第一、二、三象限的一条直线,则函数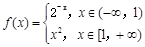 ,若
,若 ,则x的取值范围是______________.
,则x的取值范围是______________.