题目内容
(本小题满分10分)已知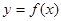 是二次函数,方程
是二次函数,方程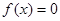 有两个相等实根,且
有两个相等实根,且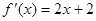 .
.
(1)求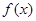 的解析式;
的解析式;
(2)求函数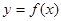 与
与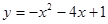 所围成图形的面积.
所围成图形的面积.
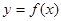 是二次函数,方程
是二次函数,方程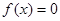 有两个相等实根,且
有两个相等实根,且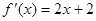 .
.(1)求
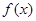 的解析式;
的解析式;(2)求函数
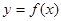 与
与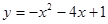 所围成图形的面积.
所围成图形的面积.(1) .
.
(2)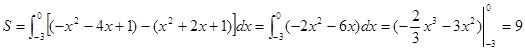
 .
.(2)
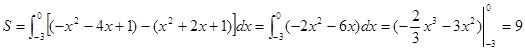
本试题主要是考查了二次函数的解析式的求解,以及二次函数的与平面图形的围成的曲边梯形面积的表示的综合运用。
(1)根据已知题意可知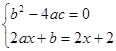 ,然后得到参数a,b,c的值
,然后得到参数a,b,c的值
(2)根据已知条件,先求解交点坐标,然后运用定积分表示其面积的值。
解:(1)设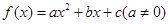 ,则
,则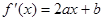 .依题意有
.依题意有
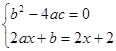 ,得
,得 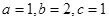 .∴
.∴ .
.
(2)由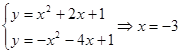 或
或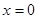 ,
,
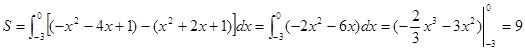
(1)根据已知题意可知
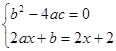 ,然后得到参数a,b,c的值
,然后得到参数a,b,c的值(2)根据已知条件,先求解交点坐标,然后运用定积分表示其面积的值。
解:(1)设
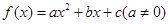 ,则
,则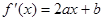 .依题意有
.依题意有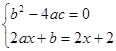 ,得
,得 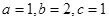 .∴
.∴ .
.(2)由
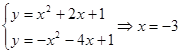 或
或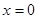 ,
,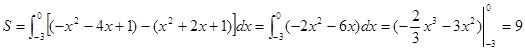

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 经过点
经过点
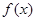 的解析式;
的解析式;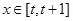 时,求
时,求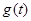 。
。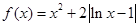 .
.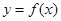 的最小值;
的最小值;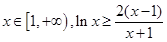 恒成立;
恒成立;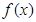 图象上的不同两点
图象上的不同两点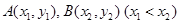 ,如果在函数
,如果在函数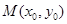 (其中
(其中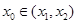 )使得点
)使得点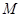 处的切线
处的切线 ,则称直线
,则称直线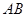 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当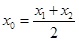 时,又称直线
时,又称直线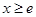 时,对于函数
时,对于函数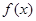 图象上不同两点
图象上不同两点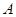 、
、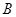 ,直线
,直线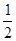 ,1]是单调函数,则a的取值范围是 ( )
,1]是单调函数,则a的取值范围是 ( )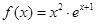 ,
,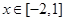 的最大值为( )
的最大值为( )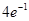
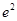
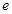

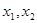 分别为三次函数
分别为三次函数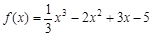 的极大值点和极小值点,则以
的极大值点和极小值点,则以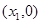 为顶点,
为顶点,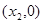 为焦点的双曲线的离心率
为焦点的双曲线的离心率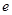 等于
等于 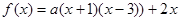 (
(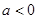 )
)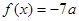 有两个相等的实数根,求
有两个相等的实数根,求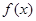 的解析式;
的解析式;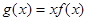 在区间
在区间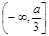 内单调递减,求a的取值范围
内单调递减,求a的取值范围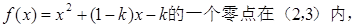 则实数k的取值范围是()
则实数k的取值范围是()