题目内容
5．设随机变量X的分布列为P（X=i）=$\frac{i}{2a}$，i=1，2，3，则P（X=2）=$\frac{1}{3}$．分析 由分布列的性质得$\frac{1}{2a}+\frac{2}{2a}+\frac{3}{2a}$=1，从而求出a=3，由此能求出P（X=2）．
解答 解：∵随机变量X的分布列为P（X=i）=$\frac{i}{2a}$，i=1，2，3，
∴$\frac{1}{2a}+\frac{2}{2a}+\frac{3}{2a}$=1，解得a=3，
∴P（X=2）=$\frac{2}{2a}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意分布列的性质的合理运用．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
15．一个容量为100的样本，其数据的分组与各组的参数如下：（0，10〕，12；（10，20〕，13；（20，30〕，15；（30，40〕，24；（40，50〕，16；（50，60〕，13；（60，70〕，7；则这样本数据落在（10，40〕上的频率为（ ）
| A． | 0.13 | B． | 0.39 | C． | 0.52 | D． | 0.64 |
16．
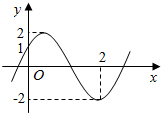函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则f（1）+f（2）+…+f（2015）的值为（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则f（1）+f（2）+…+f（2015）的值为（ ）| A． | -1 | B． | $\frac{7\sqrt{2}}{2}$ | C． | 671 | D． | 2015 |
13．向边长分别为5，5，6的三角形区域内随机投一点M，则该点M与三角形三个顶点距离都大于1的概率为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{24}$ | C． | 1-$\frac{π}{12}$ | D． | 1-$\frac{π}{24}$ |
14．若sin$\frac{α}{2}$=$\frac{1}{3}$，则cos（π+α）等于（ ）
| A． | -$\frac{7}{9}$ | B． | $\frac{7}{9}$ | C． | -$\frac{5}{9}$ | D． | $\frac{5}{9}$ |