题目内容
15.函数y=sinax+$\frac{1}{2}$与函数y=(a-1)x2+x在同一坐标系内的图象不可能是( )| A. | 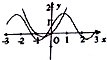 | B. | 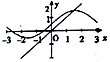 | C. |  | D. | 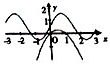 |
分析 分别令a=0,a=1,a>1,a<0.根据二次函数(或一次函数,常数函数)和三角函数的图象和性质判断即可.
解答 解:当a=1时,函数y=sinx+$\frac{1}{2}$与函数y=x,图象B符合,
当a=0时,函数y=$\frac{1}{2}$与函数y=x2+x,图象C符合,
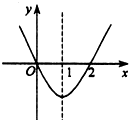
当a>1时,y=(a-1)x2+x开口向上,对称轴x=-$\frac{1}{2(a-1)}$<0,y=sinax+$\frac{1}{2}$的图象在y=sinax的基础上向上平移$\frac{1}{2}$单位,图象A符合,
当a<0时,y=(a-1)x2+x开口向下,对称轴x=-$\frac{1}{2(a-1)}$>0,y=sinax+$\frac{1}{2}$的图象在y=sin|a|x的基础上翻转180后,再向上平移$\frac{1}{2}$单位,图象D不符合,
故选:D.
点评 本题考查了图象和识别,以及二次函数和三角函数的图象和性质,属于基础题.

练习册系列答案
相关题目
6.已知A1、A2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左右顶点,双曲线C的焦距为2c,P为右支上异于A2的一点,直线PA2与直线x=$\frac{{a}^{2}}{c}$相交于点Q,若$\overrightarrow{{A}_{1}P}$•$\overrightarrow{{A}_{1}Q}$=0,则双曲线C的渐近线方程为( )
| A. | y=±2x | B. | y=±x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
3.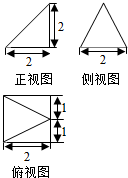 已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.
已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.
 已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.
已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 2 | D. | 4 |
10.已知非零向量$\overrightarrow{OA}$=(a,0),$\overrightarrow{OB}$=(0,a),$\overrightarrow{OC}$=(1,2),若A,B,C三点共线,则a=( )
| A. | -1 | B. | 1 | C. | 3 | D. | 0或3 |
20.已知命题p:全等三角形面积相等;命题q:矩形对角线互相垂直.下面四个结论中正确的是( )
| A. | p∧q是真命题 | B. | p∨q是真命题 | C. | ¬p是真命题 | D. | ¬q是假命题 |
4.直线3x-$\sqrt{3}y$+1=0的倾斜角为( )
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |