题目内容
5.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°.(Ⅰ)求(3$\overrightarrow{a}-\overrightarrow{b}$)$•(\overrightarrow{a}+2\overrightarrow{b})$的值;
(Ⅱ)求|$\overrightarrow{a}+\overrightarrow{b}$|的值.
分析 求解$\overrightarrow{a}$$•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos120°
(I)展开(3$\overrightarrow{a}$$-\overrightarrow{b}$)•($\overrightarrow{a}$$+2\overrightarrow{b}$)=3$\overrightarrow{a}$2$+5\overrightarrow{a}$$•\overrightarrow{b}$$-2\overrightarrow{b}$2,代入即可
(II)根据|$\overrightarrow{a}$$+\overrightarrow{b}$|=$\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}$求解.
解答 解:∵|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°
∴$\overrightarrow{a}$$•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos120°=2×$3×(-\frac{1}{2})$=-3,
(Ⅰ)(3$\overrightarrow{a}$$-\overrightarrow{b}$)•($\overrightarrow{a}$$+2\overrightarrow{b}$)=3$\overrightarrow{a}$2$+5\overrightarrow{a}$$•\overrightarrow{b}$$-2\overrightarrow{b}$2=12-15-18=-21
(Ⅱ)|$\overrightarrow{a}$$+\overrightarrow{b}$|=$\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}$=+9=$\sqrt{7}$.
点评 本题考察了平面向量的数量积的运用,向量的线性运算,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{16}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{16}{3}$π | D. | $\frac{32}{3}$π |
| A. | $\frac{1}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{4}{π}$ | D. | $\frac{π}{4}$ |
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
| A. | {x|-1<x<3} | B. | {x|0<x<3} | C. | {x|x>-1} | D. | {x|x<3} |
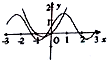
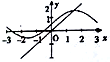
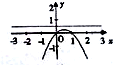
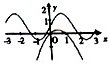
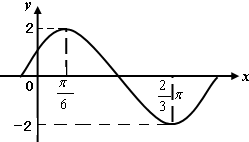 若函数f(x)=Asin(ωx+φ)的部分图象如图所示:
若函数f(x)=Asin(ωx+φ)的部分图象如图所示: