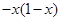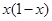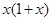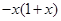题目内容
已知函数f(x)的定义域为R,且f(x)不为常值函数,有以下命题:
①函数g(x)=f(x)+f(-x)一定是偶函数;
②若对任意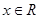 都有
都有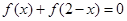 ,则f(x)是以2为周期的周期函数;
,则f(x)是以2为周期的周期函数;
③若f(x)是奇函数,且对任意x∈R都有f(x)+f(2+x)=0,则f(x)的图像的对称轴方程为
x=2n+1(n∈Z);
④对任意x1,x2∈R且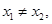 若
若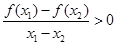 恒成立,则f(x)为
恒成立,则f(x)为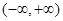 上的增函数.
上的增函数.
其中所有正确命题的序号是________________.
①函数g(x)=f(x)+f(-x)一定是偶函数;
②若对任意
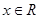 都有
都有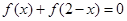 ,则f(x)是以2为周期的周期函数;
,则f(x)是以2为周期的周期函数;③若f(x)是奇函数,且对任意x∈R都有f(x)+f(2+x)=0,则f(x)的图像的对称轴方程为
x=2n+1(n∈Z);
④对任意x1,x2∈R且
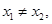 若
若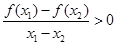 恒成立,则f(x)为
恒成立,则f(x)为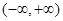 上的增函数.
上的增函数.其中所有正确命题的序号是________________.
①③④
试题分析:①
 ,所以
,所以 一定是偶函数.
一定是偶函数.②由
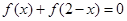 得
得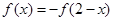 。令
。令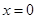 可得:
可得: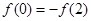 ,所以f(x)不是以2为周期的周期函数.
,所以f(x)不是以2为周期的周期函数.③f(x)是奇函数,则
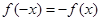 …………………………………(1)
…………………………………(1)由
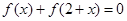 得
得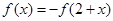 ,即
,即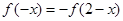 …………………………(2)
…………………………(2)由(1)(2)可得:
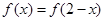 ,所以
,所以 是f(x)的图像的一条对称轴方程.
是f(x)的图像的一条对称轴方程.又由
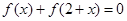 得
得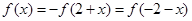 所以
所以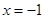 是f(x)的图像的一条对称轴方程.
是f(x)的图像的一条对称轴方程.又由
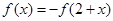 得
得 ,所以函数
,所以函数 是以4为周期的周期函数.
是以4为周期的周期函数.所以
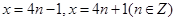 都是
都是 的对称轴,即x=2n+1 (n∈Z)是
的对称轴,即x=2n+1 (n∈Z)是 的对称轴.
的对称轴.④
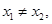 不妨设
不妨设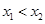 ,则由
,则由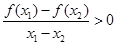 得
得 即
即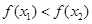 ,所以f(x)是
,所以f(x)是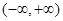 上的增函数.
上的增函数.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
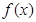 (
(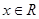 )是奇函数,函数
)是奇函数,函数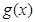 (
(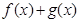 是奇函数
是奇函数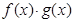 是奇函数
是奇函数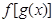 是奇函数
是奇函数 是奇函数
是奇函数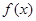 为定义在
为定义在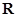 上的奇函数,当
上的奇函数,当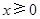 时,
时,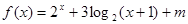 (
(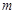 为常数),则
为常数),则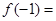 ( )
( )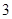
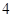
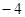
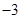
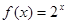 且
且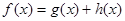 ,其中
,其中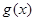 为奇函数,
为奇函数,  为偶函数,若不等式
为偶函数,若不等式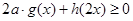 对任意
对任意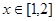 恒成立,则实数
恒成立,则实数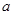 的取值范围是 .
的取值范围是 .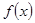 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数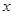 都有
都有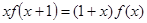 ,则
,则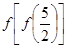 的值是( )
的值是( )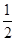
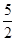
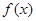 满足
满足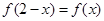 ,且在
,且在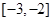 上是减函数,
上是减函数,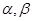 是钝角三角形的两个锐角,则下列不等式中正确的是( )
是钝角三角形的两个锐角,则下列不等式中正确的是( )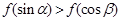

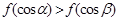
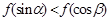
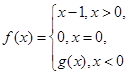 是奇函数,则
是奇函数,则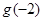 的值是 .
的值是 .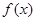 是奇函数,当
是奇函数,当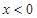 时,
时,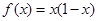 ,当
,当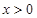 时,
时,