题目内容
20.设a,b,c为三角形的三边长,求证:$\frac{a}{1+a}$,$\frac{b}{1+b}$,$\frac{c}{1+c}$也可以构成三角形.分析 要证明:$\frac{a}{1+a}$,$\frac{b}{1+b}$,$\frac{c}{1+c}$也可以构成三角形,证明$\frac{a}{1+a}$+$\frac{b}{1+b}$>$\frac{c}{1+c}$即可.利用分析法进行证明,注意分析法的格式即可.
解答 证明:要证明:$\frac{a}{1+a}$,$\frac{b}{1+b}$,$\frac{c}{1+c}$也可以构成三角形,
证明$\frac{a}{1+a}$+$\frac{b}{1+b}$>$\frac{c}{1+c}$即可.
需证明:a(1+b)(1+c)+b(1+a)(1+c)>c(1+a)(1+b)(4分)
需证明:a(1+b+c+bc)+b(1+a+c+ac)>c(1+a+b+ab)
需证明a+2ab+b+abc>c(8分)
∵a,b,c是△ABC的三边
∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0
∴a+2ab+b+abc>c
∴$\frac{a}{1+a}$+$\frac{b}{1+b}$>$\frac{c}{1+c}$成立,
∴$\frac{a}{1+a}$,$\frac{b}{1+b}$,$\frac{c}{1+c}$也可以构成三角形.(12分)
点评 本题考查利用分析法证明不等式,解题时应注意分析法的格式.

练习册系列答案
相关题目
10.在复平面内,若z=m2(1+i)-m(4+i)-6i(i为虚数单位)所对应的点在第二象限,则实数m的取值范围为( )
| A. | (-∞,-2)∪(4,+∞) | B. | (3,4) | C. | (-2,3) | D. | (3,+∞) |
5.若集合A={y|y=2x},B={x|x2-2x-3>0,x∈R},那么A∩(∁UB)=( )
| A. | (0,3] | B. | [-1,3] | C. | (3,+∞) | D. | (0,-1)∪(3,+∞) |
12.表面积为S的五面体的每一个面都外切于半径为R的一个球,则这个五面体的体积为( )
| A. | $\frac{1}{3}$SR | B. | $\frac{3}{5}$SR | C. | $\frac{2}{3}$SR | D. | $\frac{3}{2}$SR |
9.已知P:log3(-x2-2x+3)<0,则使得P成立的一个充分不必要条件是( )
| A. | [$\frac{5}{6}$,1) | B. | (-3,1) | C. | (-∞,-$\sqrt{3}$-1)∪($\sqrt{3}$-1,+∞) | D. | (-3,-$\sqrt{3-1)}$∪($\sqrt{3}$-1,1) |

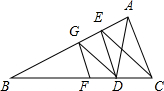 已知:△ABC中,E、G、D、F分别是边AB、CB上的一点,且GF∥ED∥AC,EF∥AD.
已知:△ABC中,E、G、D、F分别是边AB、CB上的一点,且GF∥ED∥AC,EF∥AD.