题目内容
9．已知P：log3（-x2-2x+3）＜0，则使得P成立的一个充分不必要条件是（ ）| A． | [$\frac{5}{6}$，1） | B． | （-3，1） | C． | （-∞，-$\sqrt{3}$-1）∪（$\sqrt{3}$-1，+∞） | D． | （-3，-$\sqrt{3-1）}$∪（$\sqrt{3}$-1，1） |
分析 求出P的等价条件，结合充分不必要条件的定义进行判断即可．
解答 解：由log3（-x2-2x+3）＜0，得0＜-x2-2x+3＜1，
即$\left\{\begin{array}{l}{{x}^{2}+2x-3＜0}\\{{x}^{2}+2x-2＞0}\end{array}\right.$，
即$\left\{\begin{array}{l}{-3＜x＜1}\\{x＞-1+\sqrt{3}或x＜-1-\sqrt{3}}\end{array}\right.$，
即-3＜x＜-$\sqrt{3}$-1或$\sqrt{3}$-1＜x＜1，
则P成立的一个充分不必要条件是[$\frac{5}{6}$，1），
故选：A
点评 本题主要考查充分条件和必要条件的应用，根据条件求出P的等价条件是解决本题的关键．
练习册系列答案
相关题目
14．直线y=x+b与曲线x=$\sqrt{1-{y}^{2}}$有且仅有1个公共点，则b的取值范围是（ ）
| A． | |b|=$\sqrt{2}$ | B． | -1＜b≤1或b=-$\sqrt{2}$ | C． | -1≤b≤1 | D． | -1≤b≤1 或b=$±\sqrt{2}$ |
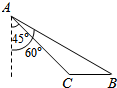如图，中国渔民在中国南海黄岩岛附近捕鱼作业，中国海监船在A地侦察发现，在南偏东60°方向的B地，有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶，企图抓捕正在C地捕鱼的中国渔民．此时，C地位于中国海监船的南偏东45°方向的10海里处，中国海监船以每小时30海里的距离赶往C地救援我国渔民，能不能及时赶到？（$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{6}$≈2.45）
18．在等差数列{an}中，${a_1}=\frac{1}{25}$，第10项开始比1大，记$t=\lim_{n→∞}\frac{{{a_n}+{S_n}}}{n^2}$，则t的取值范围是（ ）
| A． | $t＞\frac{4}{75}$ | B． | $\frac{8}{75}＜t≤\frac{3}{25}$ | C． | $\frac{4}{75}＜t＜\frac{3}{50}$ | D． | $\frac{4}{75}＜t≤\frac{3}{50}$ |
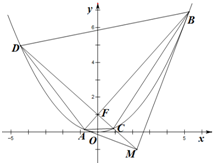已知抛物线x2=4y的焦点为F，过焦点F且不平行于x轴的动直线l交抛物线于A（x1，y1），B（x2，y2）两点，抛物线在A、B两点处的切线交于点M．