题目内容
2. 如图,已知离心率为$\frac{\sqrt{3}}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(2,1),O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A,B.
如图,已知离心率为$\frac{\sqrt{3}}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(2,1),O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A,B.(1)求椭圆C的标准方程;
(2)求△AOB面积的最大值;
(3)证明:直线MA、MB与x轴围成一个等腰三角形.
分析 (1)通过斜率、将点M代入椭圆方程,计算即得结论;
(2)通过设l方程y=$\frac{1}{2}$x+m,并与椭圆C方程联立,利用根的判别式△>0,可得m的取值范围,结合韦达定理、三角形的面积公式计算即可;
(3)问题即证直线MA、MB的斜率和为0,计算即可.
解答 (1)解:设椭圆C的方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意得:$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{4}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=8}\\{{b}^{2}=2}\end{array}\right.$,
∴椭圆方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$;
(2)解:由直线l∥OM,可设l方程:y=$\frac{1}{2}$x+m,
联立l方程与椭圆C方程,消去y整理得:x2+2mx+2m2-4=0,
设A(x1,y1),B(x2,y2),则x1+x2=-2m,x1x2=2m2-4,
由题意可得△=(2m)2-4(2m2-4)>0,
于是m∈(-2,2)且m≠0,
故S△OAB=$\frac{1}{2}$|m|•|x1-x2|
=$\frac{1}{2}$|m|•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=|m|$\sqrt{4-{m}^{2}}$
=$\sqrt{{m}^{2}(4-{m}^{2})}$
≤$\frac{{m}^{2}+4-{m}^{2}}{2}$
=2(当且仅当m2=4-m2即m=±$\sqrt{2}$时取等号),
∴△AOB面积的最大值为2;
(3)证明:设直线MA、MB的斜率分别为k1、k2,
则k1=$\frac{{y}_{1}-1}{{x}_{1}-2}$,k2=$\frac{{y}_{2}-1}{{x}_{2}-1}$,
下面只需证明:k1+k2=0,
事实上,k1+k2=$\frac{{y}_{1}-1}{{x}_{1}-2}$+$\frac{{y}_{2}-1}{{x}_{2}-1}$
=$\frac{\frac{1}{2}{x}_{1}+m-1}{{x}_{1}-2}$+$\frac{\frac{1}{2}{x}_{2}+m-1}{{x}_{2}-2}$
=1+m($\frac{1}{{x}_{1}-2}$+$\frac{1}{{x}_{2}-2}$)
=1+m•$\frac{{x}_{1}+{x}_{2}-4}{{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4}$
=1+m•$\frac{-2m-4}{2{m}^{2}-4-2(-2m)+4}$
=0,
故直线MA、MB与x轴围成一个等腰三角形.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

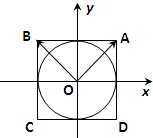 如图,在平面直角坐标系xoy中,圆x2+y2=r2(r>0)内切于正方形ABCD,任取圆上一点P,若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则$\frac{1}{4}$是m2,n2的等差中项,现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)内切于矩形ABCD,任取椭圆上一点P,若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m2,n2的等差中项为( )
如图,在平面直角坐标系xoy中,圆x2+y2=r2(r>0)内切于正方形ABCD,任取圆上一点P,若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则$\frac{1}{4}$是m2,n2的等差中项,现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)内切于矩形ABCD,任取椭圆上一点P,若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m2,n2的等差中项为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
 已知E、F是x轴上的点,坐标原点O为线段EF的中点,|$\overrightarrow{FG}|=10,|\overrightarrow{EF}$|=6,G,P是坐标平面上的动点,点P在线段FG上,EG的中点为H,且$\overrightarrow{PH}•\overrightarrow{EG}$=0.
已知E、F是x轴上的点,坐标原点O为线段EF的中点,|$\overrightarrow{FG}|=10,|\overrightarrow{EF}$|=6,G,P是坐标平面上的动点,点P在线段FG上,EG的中点为H,且$\overrightarrow{PH}•\overrightarrow{EG}$=0.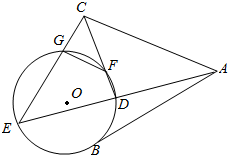 如图,AB是圆O的一条切线,切点为B,ADE,CFD,CGE都是圆O的割线,已知AC=AB.
如图,AB是圆O的一条切线,切点为B,ADE,CFD,CGE都是圆O的割线,已知AC=AB.